A light ray falls on a rectangular glass slab as shown. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is

√3/2
(√3+1)2
(√2+1)2
√5/2
The correct Answer is:A
For point A,aμg=sin45∘sint
⇒sinr=(1)(√2μg)
for point (90−r)=gμg
(90−r) is critcal angle .
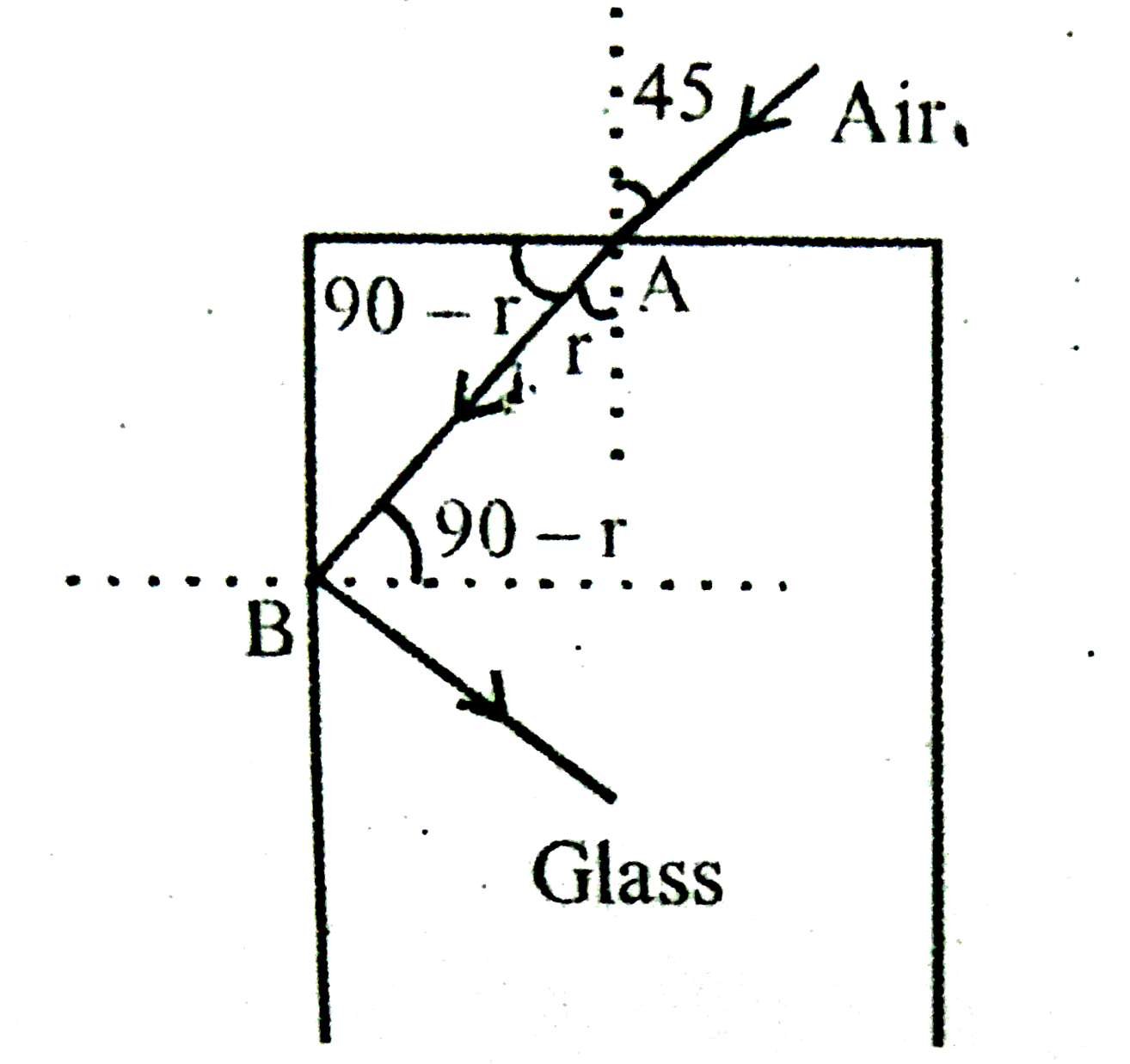
∴cosr=gμg=1aμg
⇒aμg=1cosr
⇒1√1−sin2r=1√1−12aμ2g
⇒aμ2g=11−12aμ2g=2aμ2g2aμ2g−1
⇒2aμ2g−1=2⇒aμ2g=√32
Similar Questions
For a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.

View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light falls normally on a rectangular glass slab.
Draw a ray diagram showing the path of the ray till it emerges out of the slab.
View Solution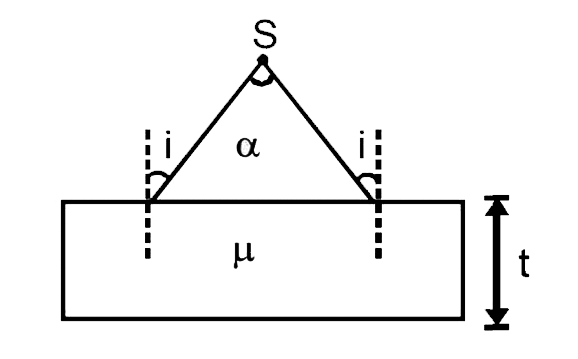
A diverging beam of light from a point source S having devergence angle α, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam is
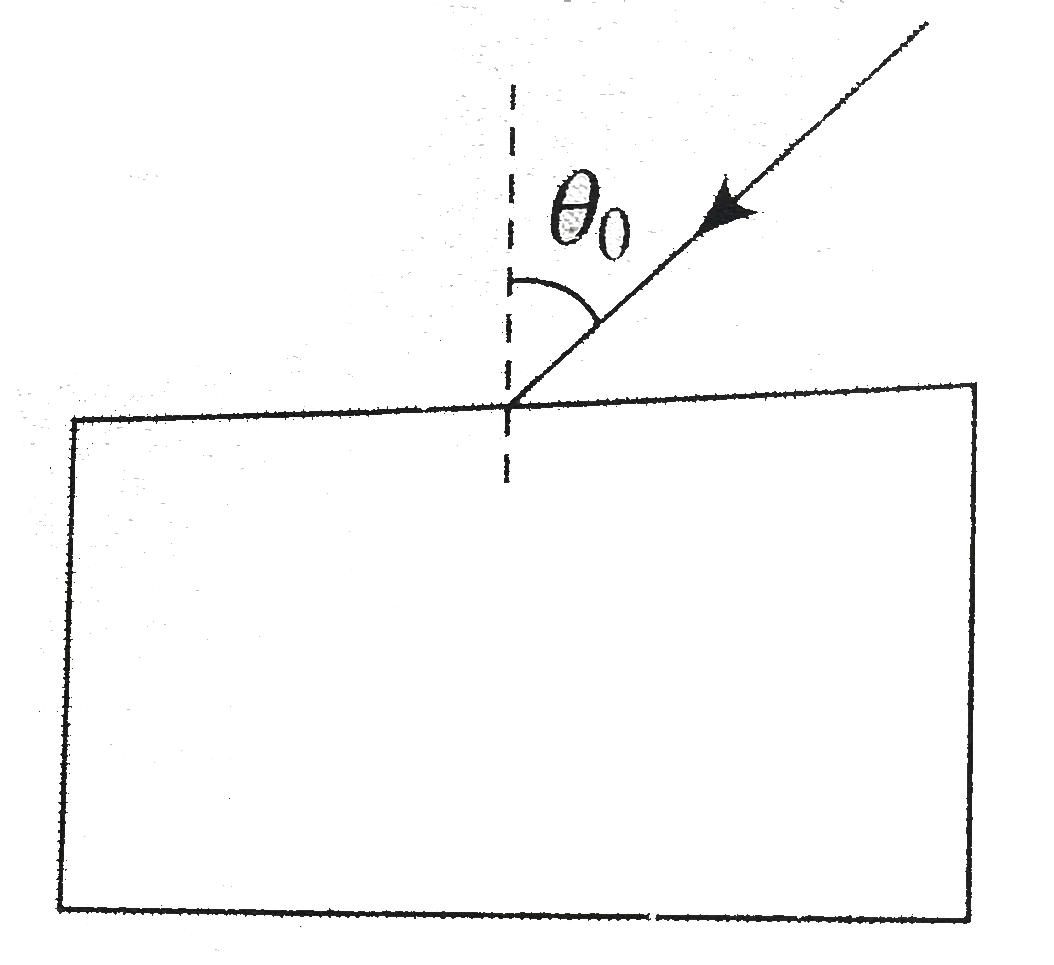
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
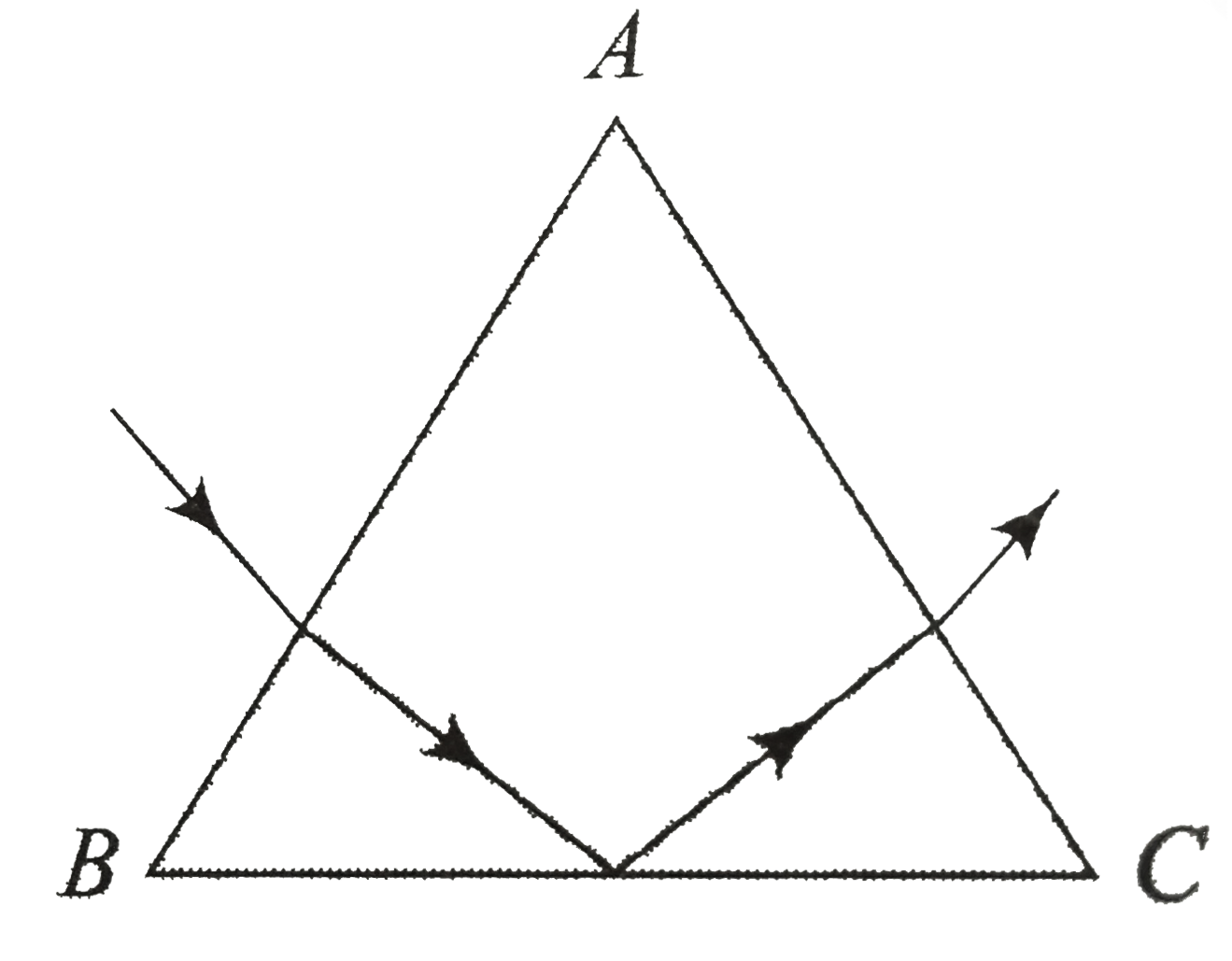
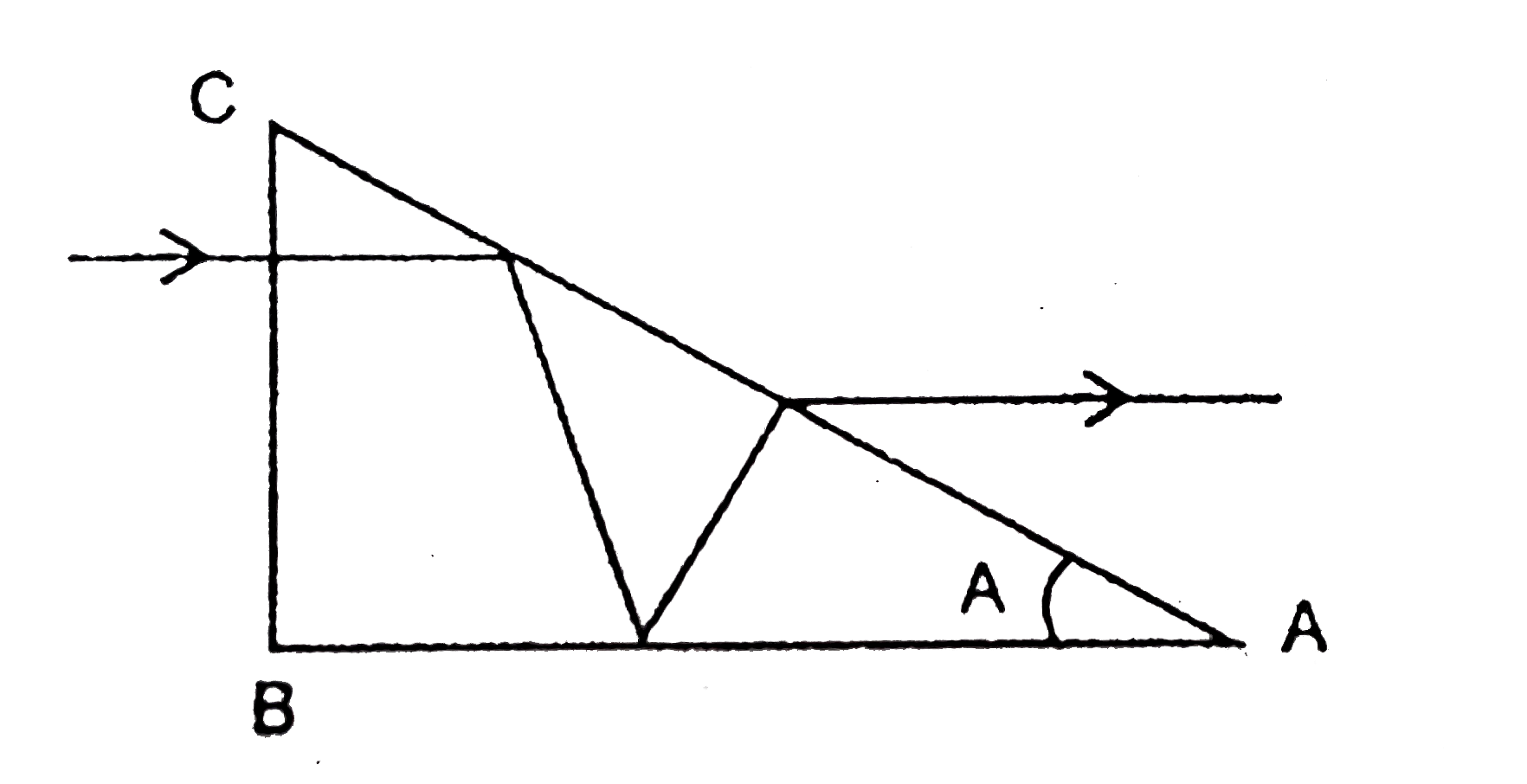
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
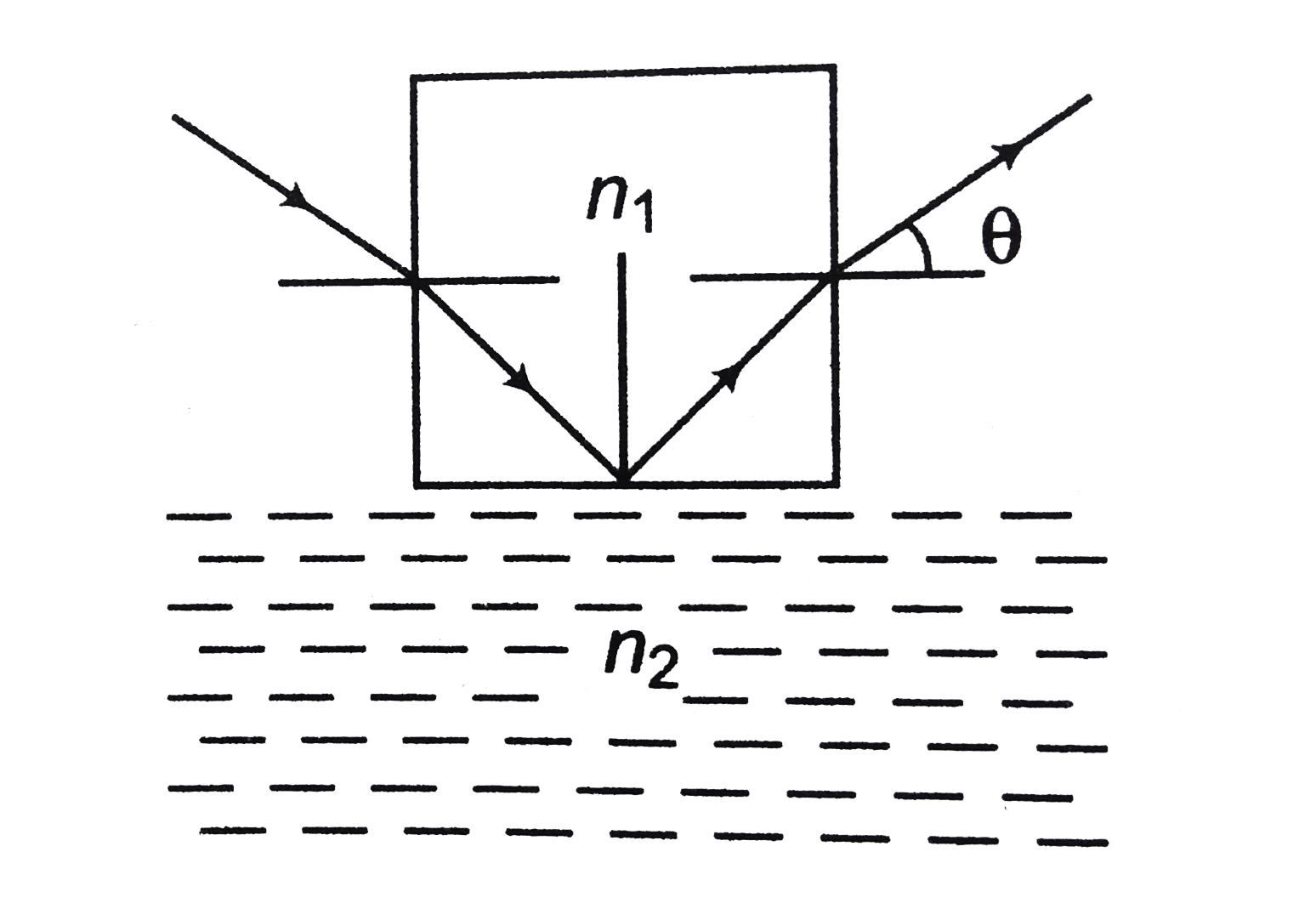
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
View SolutionLight from a luminious point on the lower face of a rectangular glass slab , 2 cm thick, strikes the upper face and the totally reflected rays outline a circle of 3.2 cm radius on the lower face. Find the refractive index of the glass.
View SolutionA ray of light falls normally on one face of a right angled prims of refracting angle A. It suffers two total internal reflections before coming out of prism parallel to incident ray as shown. Refractive index to prism material will be:
View SolutionA light ray is incident at 45∘ on a glass slab. The slab is 3cm thick, and the refractive index of the glass is 1.5. What will the displacement of the ray be as a result of its passage through the slab? At what angle will the ray emerge formn the slab?
View Solution
