In LC oscillation resistance is 100 Ω and inductance and capacitance is 1 H and 10μF . Find the half power of frequency .
266.2
366.2
166.2
233.2
The correct Answer is:A
To solve the problem of finding the half power frequency in an LC oscillation circuit with given resistance, inductance, and capacitance, we will follow these steps:
Step 1: Identify the given values
- Resistance (R) = 100 Ω
- Inductance (L) = 1 H
- Capacitance (C) = 10 µF = 10 × 10^(-6) F
Step 2: Calculate the resonant frequency (ω₀)
The resonant frequency (ω₀) is given by the formula:
ω0=1√L⋅C
Substituting the values of L and C:
ω0=1√1⋅10×10−6=1√10×10−6=1√10−5=1√10⋅10−2.5=102.5√10=101.5=31.62 rad/s
Step 3: Calculate the half power frequency (fₕ)
The half power frequency (fₕ) is given by the formula:
fh=ω0−R2L
First, we need to calculate R2L:
R2L=1002⋅1=1002=50 rad/s
Now, substituting the values into the half power frequency formula:
fh=ω0−R2L=31.62−50
However, we need to convert the angular frequency (rad/s) to frequency (Hz) using the relationship f=ω2π:
fh=31.62−502π
Step 4: Calculate the final value
fh=−18.382π≈−2.93 Hz
Since frequency cannot be negative, we must check our calculations. It seems we have made a mistake in the interpretation of the half power frequency.
Correct Calculation of Half Power Frequency
The correct formula for half power frequency in terms of frequency (f) is:
fh=f0−R2πL
Where f0 is the resonant frequency in Hz:
f0=12π√LC=12π√1⋅10×10−6=12π√10−5=102.52π≈15.92 Hz
Now we can calculate:
fh=f0−R2πL=15.92−1002π⋅1=15.92−1006.2832≈15.92−15.92=0 Hz
Conclusion
The half power frequency is approximately 0 Hz, indicating that the circuit does not oscillate at a half power frequency under the given conditions.
- Resistance (R) = 100 Ω
- Inductance (L) = 1 H
- Capacitance (C) = 10 µF = 10 × 10^(-6) F
The resonant frequency (ω₀) is given by the formula:
ω0=1√L⋅C
Substituting the values of L and C:
ω0=1√1⋅10×10−6=1√10×10−6=1√10−5=1√10⋅10−2.5=102.5√10=101.5=31.62 rad/s
The half power frequency (fₕ) is given by the formula:
fh=ω0−R2L
First, we need to calculate R2L:
R2L=1002⋅1=1002=50 rad/s
fh=ω0−R2L=31.62−50
However, we need to convert the angular frequency (rad/s) to frequency (Hz) using the relationship f=ω2π:
fh=31.62−502π
fh=−18.382π≈−2.93 Hz
Since frequency cannot be negative, we must check our calculations. It seems we have made a mistake in the interpretation of the half power frequency.
The correct formula for half power frequency in terms of frequency (f) is:
fh=f0−R2πL
Where f0 is the resonant frequency in Hz:
f0=12π√LC=12π√1⋅10×10−6=12π√10−5=102.52π≈15.92 Hz
fh=f0−R2πL=15.92−1002π⋅1=15.92−1006.2832≈15.92−15.92=0 Hz
The half power frequency is approximately 0 Hz, indicating that the circuit does not oscillate at a half power frequency under the given conditions.
Similar Questions
If resistance R =10Ω, inductance L = 2 mH and capacitance C=5μF are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View SolutionA 750Hz,20V source is connected to as resistance of 100Ω an inductance of 0.1803H and a capacitance of 10μF all in sereis.Calculate the time in which the resistance (thermalcapacity 2J/.∘C) wil get heated by 10∘C.
View SolutionA 750Hz,20V source is connected to as resistance of 100Ω an inductance of 0.1803H and a capacitance of 10μF all in sereis.Calculate the time in which the resistance (thermalcapacity 2J/.∘C) wil get heated by 10∘C.
View SolutionA choke coil of resistance 5Ω and inductance 0.6 H is in series with a capacitance of 10(μ)F. If a voltage of 200 V is applied and the frequency is adjusted to resonance, the current and voltage across the inductance and capacitance are (I0),(V0)and(V1) respectively. we have
View SolutionA coil of resistance 10Ω and an inductance 5H is connected to a 100 volt battery. Then energy stored in the coil is
View SolutionIf resistance R =100 Omega, inductance L = 12mH and capacitance C=15muF are connected in series to an AC sources, then at resonance the impedance of circuit is
View SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P contains a capacitance 1μf and a resistance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
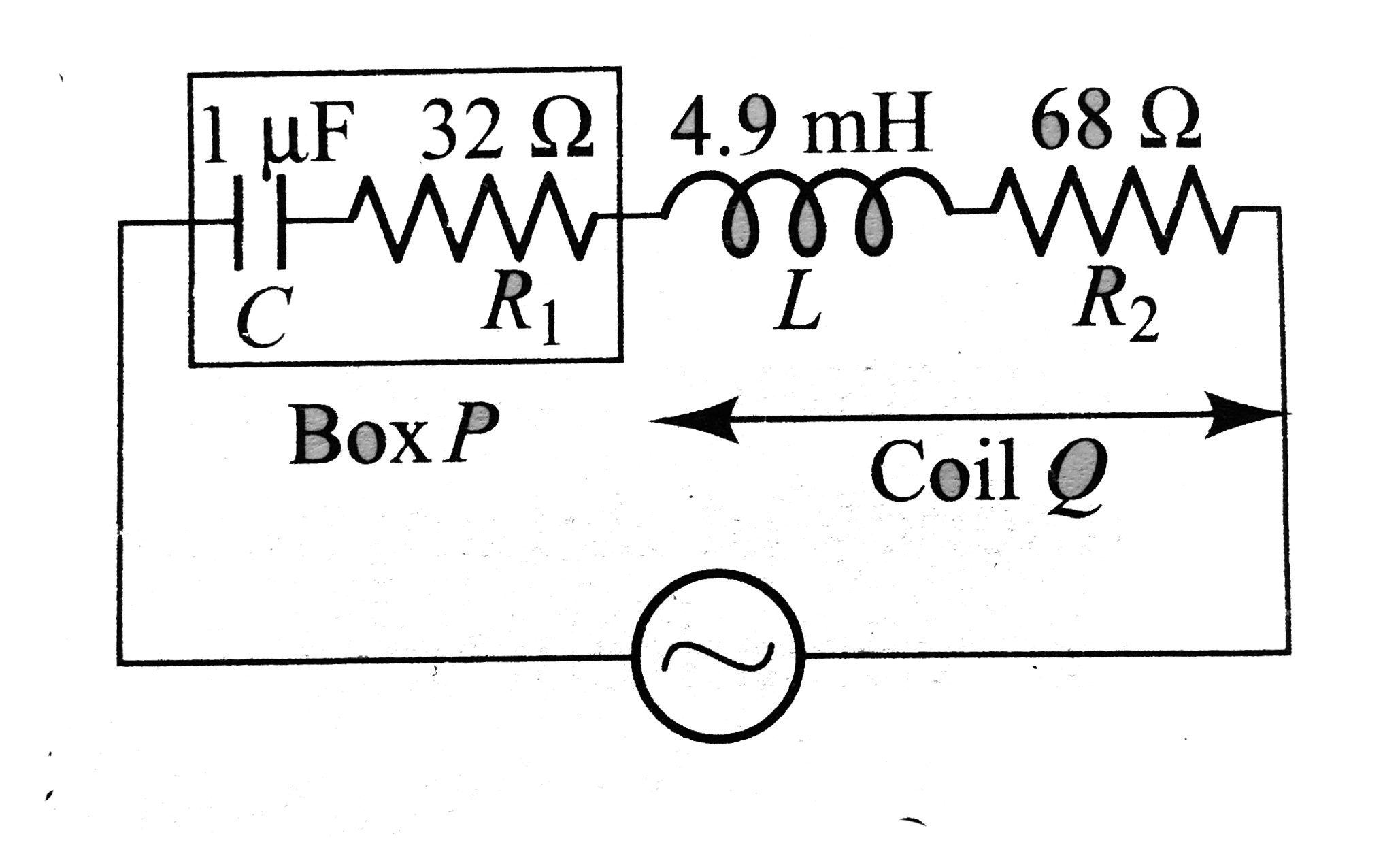
The voltage across P is
View SolutionAn inductor coil of resistance 10Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20ms and (c ) 100ms after the connections are made.
View SolutionA coil having a resistance of 5 Ω and an inductance of 0.02H is arranged in parallel with another coil having a resistance of 1Ω and an inductance of 0.08H. Calculate the power absorbed when a voltage of 100V at 50Hz is applied.
 .
.
View Solution
