An inductor coil of resistance 10Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20ms and (c ) 100ms after the connections are made.
To solve the problem, we will follow these steps:
Given Data:
- Resistance of the inductor coil, R=10Ω
- Inductance, L=120mH=120×10−3H
- EMF of the battery, E=6V
- Internal resistance of the battery, r=2Ω
Step 1: Calculate the Total Resistance
The total resistance Rtotal in the circuit is the sum of the resistance of the inductor and the internal resistance of the battery.
Rtotal=R+r=10Ω+2Ω=12Ω
Step 2: Calculate the Steady-State Current (I0)
The steady-state current I0 can be calculated using Ohm's law:
I0=ERtotal=6V12Ω=0.5A
Step 3: Calculate the Time Constant (τ)
The time constant τ for an RL circuit is given by:
τ=LRtotal=120×10−3H12Ω=10×10−3s=10ms
Step 4: Charge Flowing Through the Inductor
The charge Q that flows through the inductor at any time t is given by:
Q=I0t+τI0(e−tτ−1)
Step 5: Calculate Charge for Different Times
(a) For t=10ms
Substituting t=10×10−3s:
Q=0.5×10×10−3+10×10−3×0.5(e−1−1)
Calculating e−1≈0.3679:
Q=0.5×10×10−3+10×10−3×0.5(0.3679−1)
Q=0.005+0.005×(−0.6321)=0.005−0.0031605=0.0018395C≈1.84mC
(b) For t=20ms
Substituting t=20×10−3s:
Q=0.5×20×10−3+10×10−3×0.5(e−2−1)
Calculating e−2≈0.1353:
Q=0.01+0.005×(0.1353−1)=0.01+0.005×(−0.8647)
Q=0.01−0.0043235=0.0056765C≈5.68mC
(c) For t=100ms
Substituting t=100×10−3s:
Q=0.5×100×10−3+10×10−3×0.5(e−10−1)
Calculating e−10≈0.0000454:
Q=0.05+0.005×(0.0000454−1)=0.05+0.005×(−0.9999546)
Q=0.05−0.004999773=0.045000227C≈0.045C
Final Answers:
- (a) Charge after 10 ms: Q≈1.84mC
- (b) Charge after 20 ms: Q≈5.68mC
- (c) Charge after 100 ms: Q≈0.045C
- Resistance of the inductor coil, R=10Ω
- Inductance, L=120mH=120×10−3H
- EMF of the battery, E=6V
- Internal resistance of the battery, r=2Ω
The total resistance Rtotal in the circuit is the sum of the resistance of the inductor and the internal resistance of the battery.
Rtotal=R+r=10Ω+2Ω=12Ω
The steady-state current I0 can be calculated using Ohm's law:
I0=ERtotal=6V12Ω=0.5A
The time constant τ for an RL circuit is given by:
τ=LRtotal=120×10−3H12Ω=10×10−3s=10ms
The charge Q that flows through the inductor at any time t is given by:
Q=I0t+τI0(e−tτ−1)
(a) For t=10ms
Substituting t=10×10−3s:
Q=0.5×10×10−3+10×10−3×0.5(e−1−1)
Calculating e−1≈0.3679:
Q=0.5×10×10−3+10×10−3×0.5(0.3679−1)
Q=0.005+0.005×(−0.6321)=0.005−0.0031605=0.0018395C≈1.84mC
Substituting t=20×10−3s:
Q=0.5×20×10−3+10×10−3×0.5(e−2−1)
Calculating e−2≈0.1353:
Q=0.01+0.005×(0.1353−1)=0.01+0.005×(−0.8647)
Q=0.01−0.0043235=0.0056765C≈5.68mC
Substituting t=100×10−3s:
Q=0.5×100×10−3+10×10−3×0.5(e−10−1)
Calculating e−10≈0.0000454:
Q=0.05+0.005×(0.0000454−1)=0.05+0.005×(−0.9999546)
Q=0.05−0.004999773=0.045000227C≈0.045C
- (a) Charge after 10 ms: Q≈1.84mC
- (b) Charge after 20 ms: Q≈5.68mC
- (c) Charge after 100 ms: Q≈0.045C
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuitView SolutionA coil of resistance 10Ω and an inductance 5H is connected to a 100 volt battery. Then energy stored in the coil is
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The current in the circuit in steady state.View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
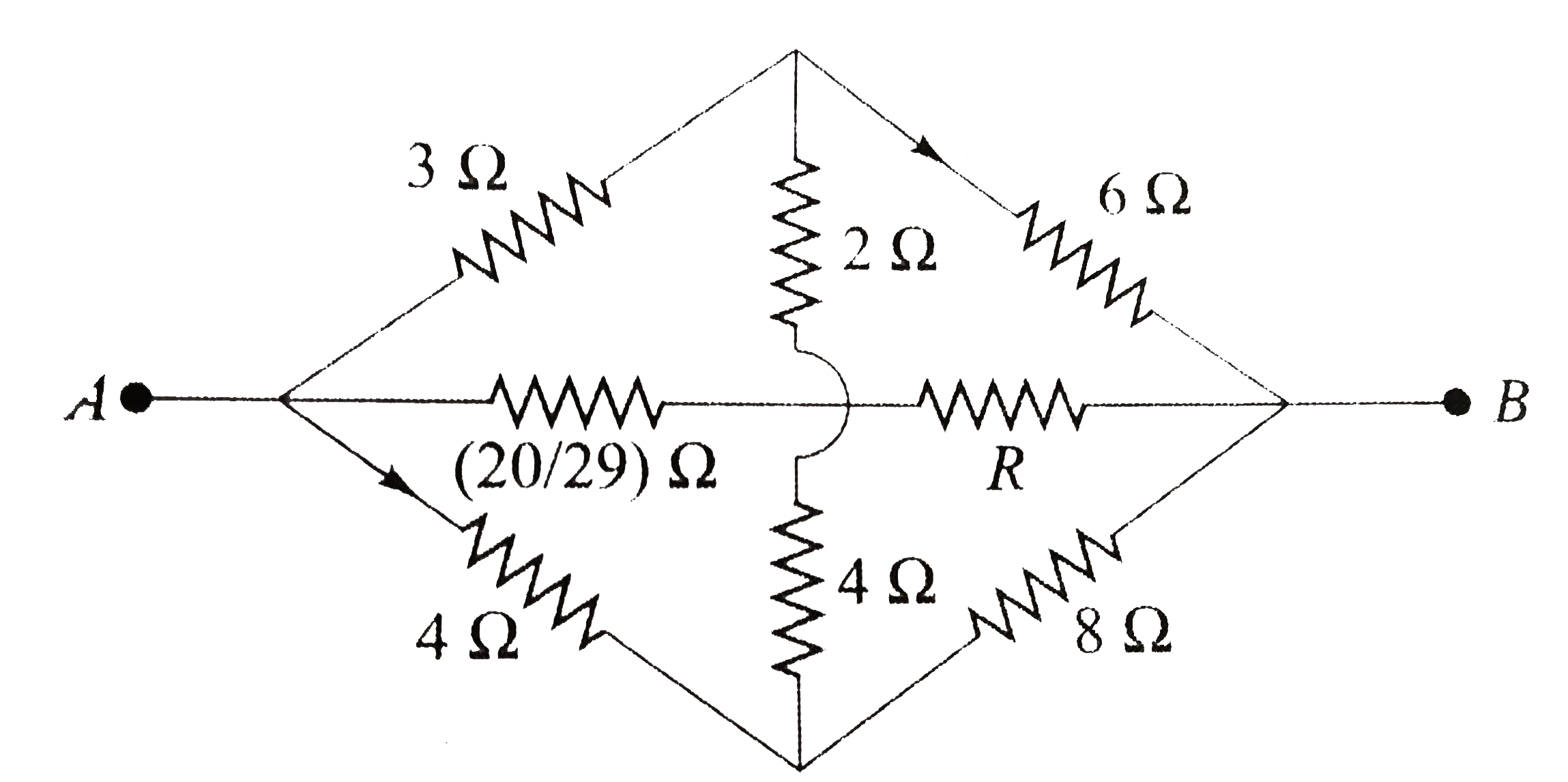 . View Solution
. View SolutionA 10 V cell of neglible internal resitsance is connected in parallel across a battery of emf 200 V and internal resistance 38Ω as shown in the figure. Find the value of current in the circuit.
 View Solution
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(ii) time at which the rate has time miximum value isView SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View Solution

