In LCR series circuit source voltage is 120 volt and voltage in inductor 50 volt and resistance is 40 volt then determine voltage in capacitor.
VC=10(5−8√2)
VC=10(5+8√2)
VC=20(5+8√2)
VC=10(5+7√2)
The correct Answer is:B
To solve the problem step by step, we can use the relationship between the voltages in an LCR series circuit. The total voltage in the circuit is equal to the vector sum of the voltages across the resistor (Vr), inductor (Vl), and capacitor (Vc).
Step 1: Understand the relationship
In an LCR series circuit, the source voltage (Vs) is given by:
Vs=Vr+Vl−Vc
Where:
- Vs = Source voltage
- Vr = Voltage across the resistor
- Vl = Voltage across the inductor
- Vc = Voltage across the capacitor
Step 2: Substitute the known values
From the problem, we know:
- Vs=120V
- Vl=50V
- Vr=40V
Substituting these values into the equation:
120=40+50−Vc
Step 3: Simplify the equation
Now, simplify the equation:
120=90−Vc
Step 4: Solve for Vc
Rearranging the equation to solve for Vc:
Vc=90−120
Vc=−30V
Step 5: Interpret the result
The negative sign indicates that the voltage across the capacitor is 30 volts, but it is opposite in phase to the voltage across the inductor.
Final Answer
The voltage across the capacitor Vc is 30V.
---
In an LCR series circuit, the source voltage (Vs) is given by:
Vs=Vr+Vl−Vc
Where:
- Vs = Source voltage
- Vr = Voltage across the resistor
- Vl = Voltage across the inductor
- Vc = Voltage across the capacitor
From the problem, we know:
- Vs=120V
- Vl=50V
- Vr=40V
120=40+50−Vc
Now, simplify the equation:
120=90−Vc
Rearranging the equation to solve for Vc:
Vc=90−120
Vc=−30V
The negative sign indicates that the voltage across the capacitor is 30 volts, but it is opposite in phase to the voltage across the inductor.
The voltage across the capacitor Vc is 30V.
Similar Questions
Knowledge Check
- Question 1 - Select One
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is
A30∘B45∘C60∘D0∘
In a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
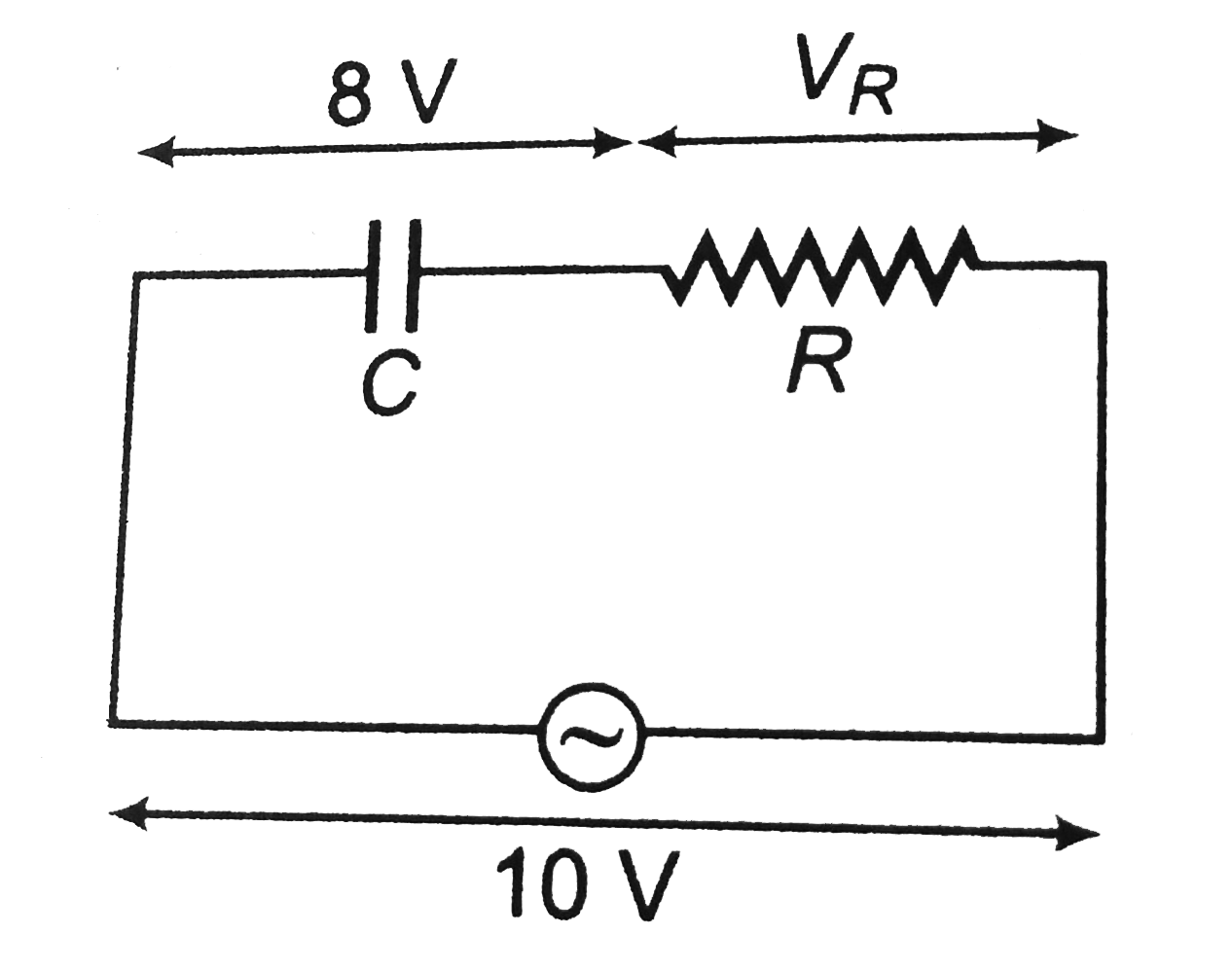 .View Solution
.View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
 .View Solution
.View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionIn series LCR AC circuit, the voltage of the source at any instant is equal to
View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
View SolutionIn a series RLC circuit the r.m.s. voltage across the resistor and the inductor are respectively 400 V and 700 V. If the equation for the applied Voltage is ε=500√2sinωt. then the peak voltage across the capacitor is
 View Solution
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
View Solution

