Establish the relation between 'g' and 'G' .
To establish the relation between 'g' (acceleration due to gravity) and 'G' (universal gravitational constant), we can follow these steps:
1. Understanding the Definitions:
- Let 'g' be the acceleration due to gravity at a distance 'r' from the center of a mass 'M' (like the Earth).
- Let 'G' be the universal gravitational constant, which quantifies the strength of the gravitational force between two masses.
2. Force due to Gravity:
- The force acting on an object of mass 'm' due to gravity can be expressed as:
F=mg
- Here, 'F' is the gravitational force, 'm' is the mass of the object, and 'g' is the acceleration due to gravity.
3. Gravitational Force Between Two Masses:
- According to Newton's law of universal gravitation, the gravitational force 'F' between two masses 'm' and 'M' separated by a distance 'r' is given by:
F=G⋅m⋅Mr2
- Here, 'G' is the universal gravitational constant, 'm' is the mass of the object, 'M' is the mass of the larger body (like Earth), and 'r' is the distance from the center of the mass 'M'.
4. Equating the Two Forces:
- Since both expressions represent the gravitational force acting on the mass 'm', we can set them equal to each other:
mg=G⋅m⋅Mr2
5. Simplifying the Equation:
- We can cancel 'm' from both sides of the equation (assuming m ≠ 0):
g=G⋅Mr2
6. Final Relation:
- Thus, the relation between 'g' and 'G' can be expressed as:
g=G⋅Mr2
- This equation shows how the acceleration due to gravity 'g' at a distance 'r' from the center of a mass 'M' is related to the universal gravitational constant 'G'.
- Let 'g' be the acceleration due to gravity at a distance 'r' from the center of a mass 'M' (like the Earth).
- Let 'G' be the universal gravitational constant, which quantifies the strength of the gravitational force between two masses.
- The force acting on an object of mass 'm' due to gravity can be expressed as:
F=mg
- Here, 'F' is the gravitational force, 'm' is the mass of the object, and 'g' is the acceleration due to gravity.
- According to Newton's law of universal gravitation, the gravitational force 'F' between two masses 'm' and 'M' separated by a distance 'r' is given by:
F=G⋅m⋅Mr2
- Here, 'G' is the universal gravitational constant, 'm' is the mass of the object, 'M' is the mass of the larger body (like Earth), and 'r' is the distance from the center of the mass 'M'.
- Since both expressions represent the gravitational force acting on the mass 'm', we can set them equal to each other:
mg=G⋅m⋅Mr2
- We can cancel 'm' from both sides of the equation (assuming m ≠ 0):
g=G⋅Mr2
- Thus, the relation between 'g' and 'G' can be expressed as:
g=G⋅Mr2
- This equation shows how the acceleration due to gravity 'g' at a distance 'r' from the center of a mass 'M' is related to the universal gravitational constant 'G'.
Topper's Solved these Questions
Similar Questions
Knowledge Check
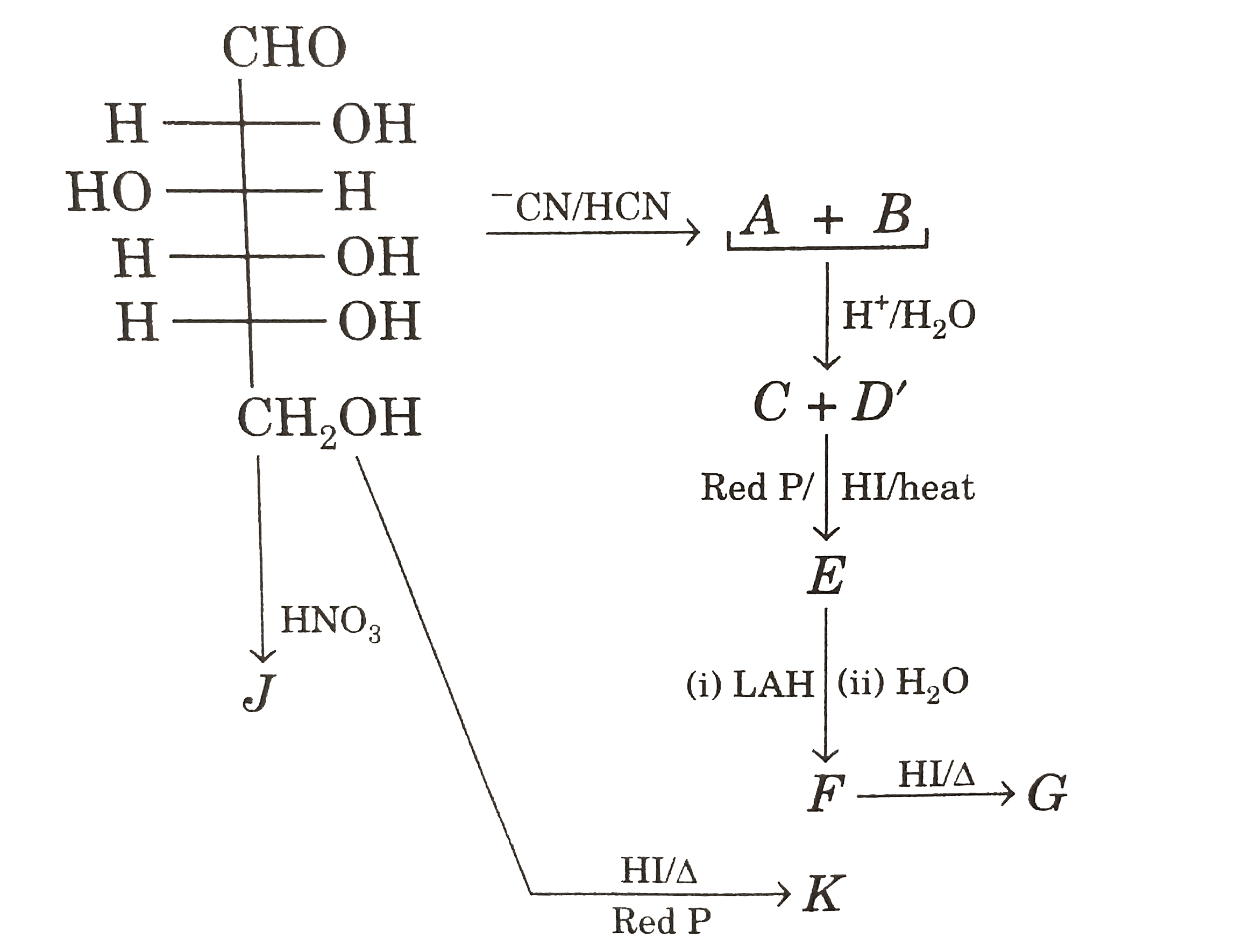
What is relation between G and K?AChain isomerBpositional isomerCHomologueDNone of these
How does the speaker establish a relation between 'me' and 'you?
View SolutionWhat is meant by giga, micro and femto ? Establish the relation between them.
View SolutionEstablish the relation between moment of inertia and torque on a rigid body
View SolutionEstablish a relation between torque and moment of inertia of a rigid body.
View SolutionWhat is drift velocity? Establish a relation between current and drift velocity?
View SolutionEstablish a relation between E.M.F. and potential difference of a cell.
View SolutionState and explain first law of thermodynamics. Establish the relation between two principle specific heats of a gas on the basis of this law.
View Solution
