Find the value of 'g'.
To find the value of 'g', which represents the acceleration due to gravity, we can use the formula derived from Newton's law of universal gravitation:
g=G⋅MR2
Where:
- G is the gravitational constant, approximately 6.67×10−11N m2/kg2
- M is the mass of the Earth, approximately 5.972×1024kg
- R is the radius of the Earth, approximately 6371km (which we need to convert to meters)
1. Identify the values needed:
- Gravitational constant G=6.67×10−11N m2/kg2
- Mass of the Earth M=5.972×1024kg
- Radius of the Earth R=6371km=6371×103m=6.371×106m
2. Plug the values into the formula:
g=G⋅MR2
g=(6.67×10−11)⋅(5.972×1024)(6.371×106)2
3. Calculate R2:
R2=(6.371×106)2=4.058×1013m2
4. Calculate the numerator:
G⋅M=(6.67×10−11)⋅(5.972×1024)≈3.986×1014N m2/kg
5. Now substitute back into the equation for g:
g=3.986×10144.058×1013≈9.81m/s2
6. Round off the value:
- The approximate value of g is often rounded to 9.8m/s2 for practical purposes.
Final Answer:
The value of g is approximately 9.8m/s2.
- G is the gravitational constant, approximately 6.67×10−11N m2/kg2
- M is the mass of the Earth, approximately 5.972×1024kg
- R is the radius of the Earth, approximately 6371km (which we need to convert to meters)
- Gravitational constant G=6.67×10−11N m2/kg2
- Mass of the Earth M=5.972×1024kg
- Radius of the Earth R=6371km=6371×103m=6.371×106m
g=G⋅MR2
g=(6.67×10−11)⋅(5.972×1024)(6.371×106)2
R2=(6.371×106)2=4.058×1013m2
G⋅M=(6.67×10−11)⋅(5.972×1024)≈3.986×1014N m2/kg
g=3.986×10144.058×1013≈9.81m/s2
- The approximate value of g is often rounded to 9.8m/s2 for practical purposes.
The value of g is approximately 9.8m/s2.
Topper's Solved these Questions
Similar Questions
(i) Determine whether f(x)=2x+34 for f:R→R is invertible or not If so find it.
(ii) Let f(x)=x2+2x,x≥−1 . Draw graph of f−1(x) also find the number of solutions of the equation f(x)=f−1(x)
(iii) If y=f(x)=x2−3x+2,x≤1.Find the value of g'(2) where g is inverse of f
View SolutionIf −27,x,−72 are in G.P. Find the value of x.
View Solution
Knowledge Check
Find the value of 8g23−2g+7 when g=3
A9B25C17D26a#b=(−1)ab(ab+ba)
f(x)=x2−2xifx≥0
=0ifx<0
g(x)=2x,ifx≥0
=1,ifx<0
Find the value of f(g(2#3))+g(f(1#2)):A9401B1049C1094Dnone of these
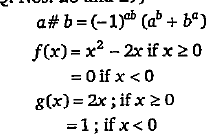
Find the value of f(g(2#3)+g(f(1#2) :
View SolutionIf f(a,b)=a+b2
g(a,b)=a2+b2
h(a,b)=max (a,b)
Find the value of f(g(3,9)),h(−1,1)
View SolutionA students forgot the product rule for differentiation and made the mistake of thinking that (f.g)'=f'g'. However he was lucky to get the correct answer. The function f that he used was f(x)=ex2 If the domain of g(x) was the interval (12,∞)with g(1)=e. Find the value of g(5).
View SolutionLet f:R→R be defined as f(x)=(2x–37)2+4x3+cosx and g=f−1, then find the value of 7g'(2π)+3g''(2π).
View SolutionThe block is always at rest, the maximum force which can be applied for this is 24x. Find the value of x. Take g = 10 m/s2{coefficient of friction = 0.3}
View SolutionFind the value of a' if (2a+1),a,(3a+2) are in G.P?
View Solution