When the remainder obtained on dividing 80808 by 108 is divided by the remainder obtained on dividing 90909 by 109, then the quotient is
8
12
3
6
The correct Answer is:A
To solve the problem step by step, we will first find the remainders when dividing 80808 by 108 and 90909 by 109. Then, we will divide the two remainders to find the quotient.
Step 1: Divide 80808 by 108
1. Perform the division:
- 80808 ÷ 108
- The first estimate is 7 (since 108 * 7 = 756).
- Subtract 756 from 80808:
80808−756=80052
- Bring down the next two digits (0) to get 800520.
- The next estimate is 4 (since 108 * 4 = 432).
- Subtract 432 from 800520:
800520−432=800088
- Bring down the next two digits (8) to get 8000888.
- The next estimate is 8 (since 108 * 8 = 864).
- Subtract 864 from 8000888:
8000888−864=8000024
2. Finding the remainder:
- The remainder when 80808 is divided by 108 is 24.
Step 2: Divide 90909 by 109
1. Perform the division:
- 90909 ÷ 109
- The first estimate is 8 (since 109 * 8 = 872).
- Subtract 872 from 90909:
90909−872=90037
- Bring down the next two digits (0) to get 900370.
- The next estimate is 3 (since 109 * 3 = 327).
- Subtract 327 from 900370:
900370−327=900043
- Bring down the next two digits (9) to get 9000439.
- The next estimate is 4 (since 109 * 4 = 436).
- Subtract 436 from 9000439:
9000439−436=9000003
2. Finding the remainder:
- The remainder when 90909 is divided by 109 is 2.
Step 3: Divide the remainders
Now we will divide the remainder obtained from the first division by the remainder obtained from the second division:
Quotient=Remainder from 80808Remainder from 90909=243=8
Final Answer
The quotient is 8.
---
- 80808 ÷ 108
- The first estimate is 7 (since 108 * 7 = 756).
- Subtract 756 from 80808:
80808−756=80052
- Bring down the next two digits (0) to get 800520.
- The next estimate is 4 (since 108 * 4 = 432).
- Subtract 432 from 800520:
800520−432=800088
- Bring down the next two digits (8) to get 8000888.
- The next estimate is 8 (since 108 * 8 = 864).
- Subtract 864 from 8000888:
8000888−864=8000024
- The remainder when 80808 is divided by 108 is 24.
- 90909 ÷ 109
- The first estimate is 8 (since 109 * 8 = 872).
- Subtract 872 from 90909:
90909−872=90037
- Bring down the next two digits (0) to get 900370.
- The next estimate is 3 (since 109 * 3 = 327).
- Subtract 327 from 900370:
900370−327=900043
- Bring down the next two digits (9) to get 9000439.
- The next estimate is 4 (since 109 * 4 = 436).
- Subtract 436 from 9000439:
9000439−436=9000003
- The remainder when 90909 is divided by 109 is 2.
Similar Questions
Knowledge Check
When the remainder obtained by dividing 60606 by 106 is subtracted from the remainder obtained on dividing 70707 by 107, then the resultant number is
A7B8C5D8When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When
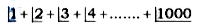 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7
When 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen 355 is divided by 82, the remainder obtained is ?
View Solution

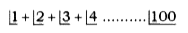 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?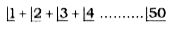 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?