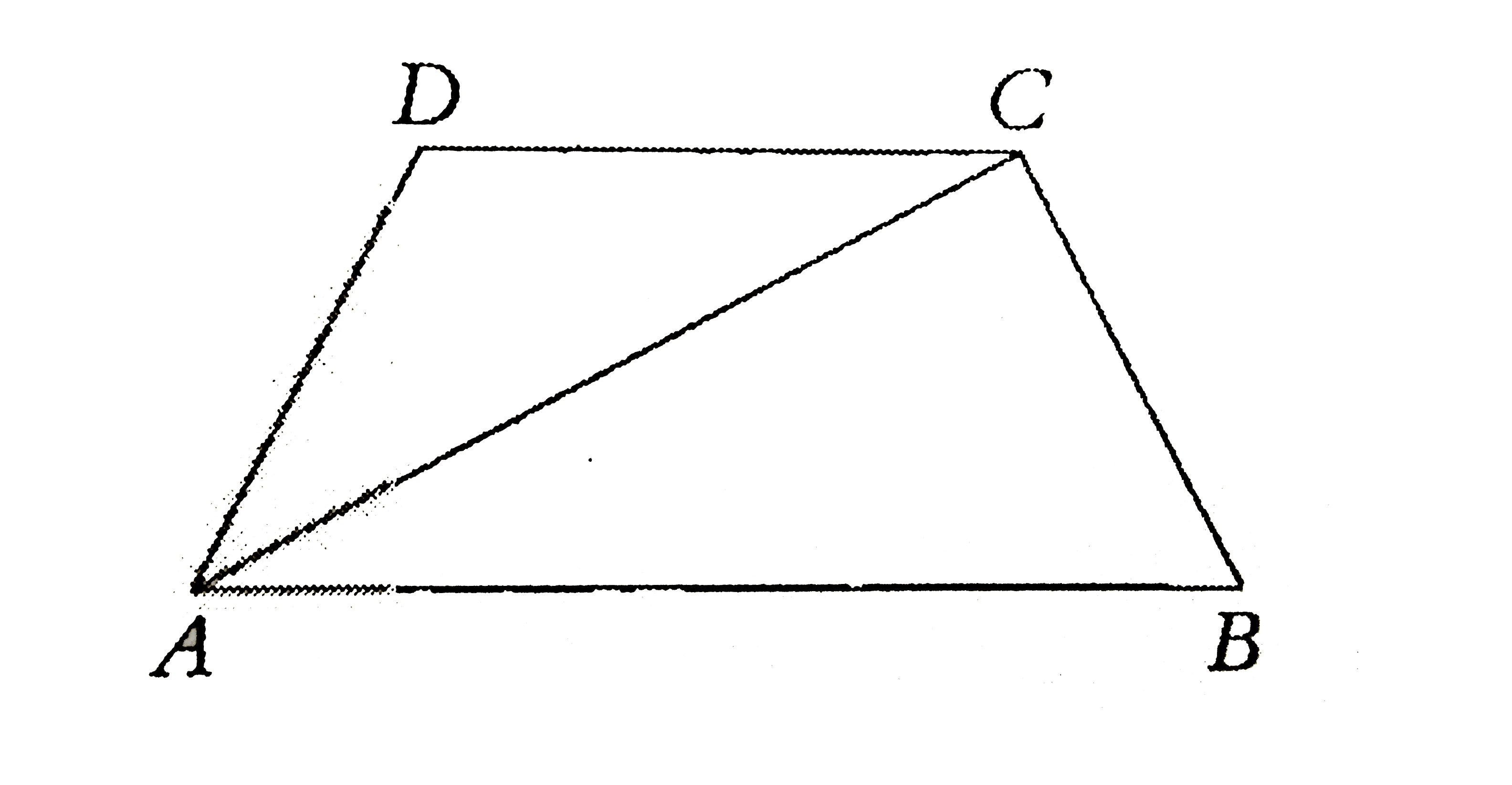
ABCD is an isosceles trapezium in which ¯¯¯¯¯¯AB||¯¯¯¯¯¯CDand∠A=57∘ . Find the value of ∠C+∠D.
112∘
123∘
246∘
303∘
The correct Answer is:C
To solve the problem, we need to find the value of ∠C+∠D in the isosceles trapezium ABCD, where ¯¯¯¯¯¯¯¯AB∥¯¯¯¯¯¯¯¯¯CD and ∠A=57∘.
1. Identify the Properties of Isosceles Trapezium:
In an isosceles trapezium, the angles on the same side of the trapezium are equal. Therefore, we have:
∠A=∠Band∠C=∠D
2. Use the Supplementary Angle Property:
Since ¯¯¯¯¯¯¯¯AB∥¯¯¯¯¯¯¯¯¯CD, the co-interior angles are supplementary. This means:
∠A+∠D=180∘
and
∠B+∠C=180∘
3. Substituting the Known Angle:
We know that ∠A=57∘. Therefore, we can substitute this value into the equation:
57∘+∠D=180∘
4. Solve for Angle D:
To find ∠D, we rearrange the equation:
∠D=180∘−57∘=123∘
5. Finding Angle C:
Since ∠C=∠D in an isosceles trapezium, we have:
∠C=123∘
6. Calculate ∠C+∠D:
Now we can find the sum of angles C and D:
∠C+∠D=123∘+123∘=246∘
Final Answer:
∠C+∠D=246∘
In an isosceles trapezium, the angles on the same side of the trapezium are equal. Therefore, we have:
∠A=∠Band∠C=∠D
Since ¯¯¯¯¯¯¯¯AB∥¯¯¯¯¯¯¯¯¯CD, the co-interior angles are supplementary. This means:
∠A+∠D=180∘
and
∠B+∠C=180∘
We know that ∠A=57∘. Therefore, we can substitute this value into the equation:
57∘+∠D=180∘
To find ∠D, we rearrange the equation:
∠D=180∘−57∘=123∘
Since ∠C=∠D in an isosceles trapezium, we have:
∠C=123∘
Now we can find the sum of angles C and D:
∠C+∠D=123∘+123∘=246∘
∠C+∠D=246∘
Topper's Solved these Questions
- MOCK TEST PAPERBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TEST PAPEREXERCISE - Questions
5 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Concept Application (Level 3 )
8 Videos
- PERCENTAGESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERCENTAGESEXERCISE - Concept Application (LEVEL 3)
7 Videos
Similar Questions
Knowledge Check
Given a trapezium ABCD in which AB||CD and AD = BC. If ∠C=76∘, then ∠D equals
A14∘B104∘C76∘Dnone of theseABCD is a cyclic trapezium such that AD || BC. If ∠ABC=70∘, then the value of ∠BCD is :
A60∘B70∘C40∘D80∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘
ABCD is a cyclic trapezium , in which AB||DC. If ∠B=75∘ , then find other angles.
View SolutionABCD is a trapezium in which AB∣∣DC and ∠A=∠B=40∘. Find ∠C and ∠D. Are these angles equal?
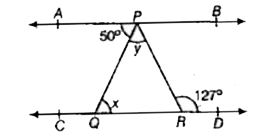
View SolutionIn figure , if AB ||CD, ∠APQ,=50∘and∠PRD=127∘ , find the value of x and y
View SolutionABCD is an isosceles trapezium . ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. AE and BF are the perpendicular drawn to CD. The congruence property used to prove the congurence of triangles AED and BFC is ______
View SolutionIn an isosceles trapezium ABCD, ∠C is equal to:

View Solution