Consider two coherent sources S(1) and S(2) producing monochromatic wa

Class 12 PHYSICS WAVE OPTICS AND INTERFERENCE

Similar Questions

Consider two coherent sources $S_{1} and S_{2}$ producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by $S_{1}$ be given by
and the displacement by $S_{2} be Y_{1} = a cos ω t$
$Y_{2} = a cos (ω t - ϕ)$
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
$I = 4 a^{2} {cos}^{2} ϕ / 2$
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
$∠ i + ∠ e = ∠ A + ∠ δ$
Where $δ$ and e denote the angle of deviation and angle of emergence respectively.

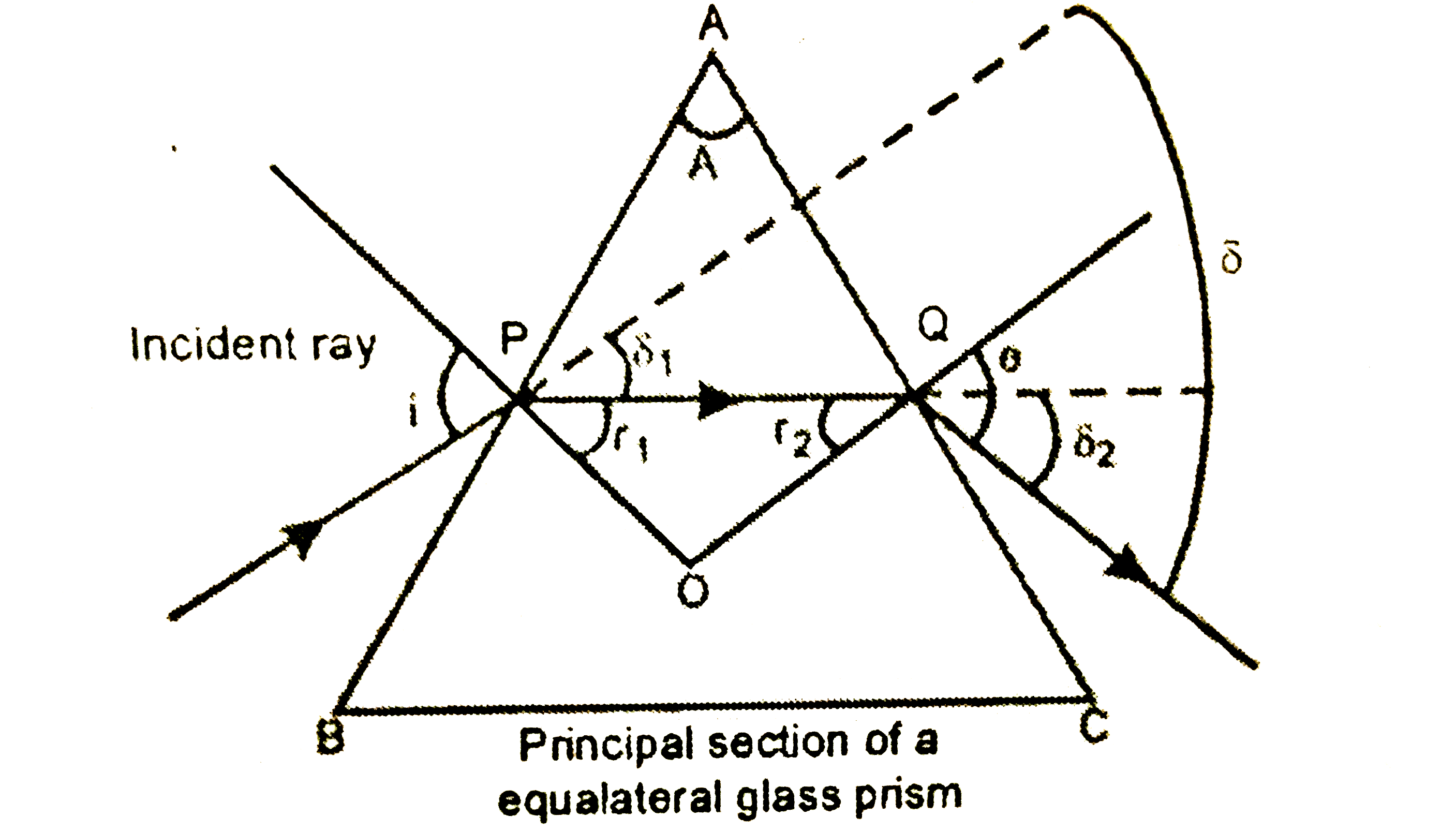
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which $∠ δ$ is minimum.
(b) Find out the relation between the refractive index $(μ)$ of the glass prism and $∠ A$ for the case when the angle of prism (A) is equal to the angle of minimum deviation $(δ_{m})$ . Hence obtain the value of the refractive index for angle $A e = 60^{\circ}$ .
View Solution
Two coherent sources of intensities $I_{1}$ and $I_{2}$ produce an interference pattern. The maximum intensity in the interference pattern will be
View Solution

Knowledge Check

The displacement of two coherent light waves are given by $y_{1} = a_{1} cos ω t and y_{2} = a_{2} cos (π / 2 - ω t)$ . The resultant intensity is given by
A $a_{1} - a_{2}$
B $a_{1} + a_{2}$
C $(a_{1}^{2} + a_{2}^{2})$
D $(a_{1}^{2} - a_{2}^{2})$
Two coherent sources of intensities $I_{1}$ and $I_{2}$ produce an interference pattern. The maximum intensity in the interference pattern will be
A(a) $I_{1} + I_{2}$
B(b) $I_{1}^{2} + I_{2}^{2}$
C(c) ${(I_{1} + I_{2})}_{1}^{2}$
D(d) ${(\sqrt{I_{1}} + \sqrt{I_{2}})}^{2}$
it the two waves represented dy $y_{1} = 4 cos ω t$ and $y_{2} = 3 cos (ω t + π / 3)$ interfere at a point, then the amplitude of the resulting wave will be about
A7
B5
C6
D $3.5$

Similar Questions

Knowledge Check

The displacement of two coherent light waves are given by y1=a1cosωtandy2=a2cos(π/2−ωt). The resultant intensity is given by

Two coherent sources of intensities I1 and I2 produce an interference pattern. The maximum intensity in the interference pattern will be

it the two waves represented dy y1=4cosωt and y2=3cos(ωt+π/3) interfere at a point, then the amplitude of the resulting wave will be about

Recommended Questions

The displacement of two coherent light waves are given by $y_{1} = a_{1} cos ω t and y_{2} = a_{2} cos (π / 2 - ω t)$ . The resultant intensity is given by

Two coherent sources of intensities $I_{1}$ and $I_{2}$ produce an interference pattern. The maximum intensity in the interference pattern will be

it the two waves represented dy $y_{1} = 4 cos ω t$ and $y_{2} = 3 cos (ω t + π / 3)$ interfere at a point, then the amplitude of the resulting wave will be about