A spherically symmetric gravitational system of particles has a mass density
ρ for r≤R0 for r>R
Where ρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field or particles. Its speed v as a functional of distance r (0ltrlt∞) from the centre of the system is represented by Solution in Marathi
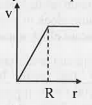
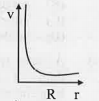
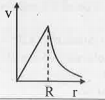
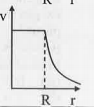
Step by step video & image solution for A spherically symmetric gravitational system of particles has a mass density overset(rho" for "rleR) underset(0" for "rgtR) Where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field or particles. Its speed v as a functional of distance r (0ltrltoo) from the centre of the system is represented by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A body while sliding went straight down an incline of 45∘ to the horizontal and was subjected to a coefficient of kinetic friction of 0.20. Starting from rest, hwo long did it take him to reach a speed of 50km/hr? (Ignore air resistance and take h=10m/s2)
View SolutionWhen a bus suddenly takes a turn, the passengers are thrown outwards because of
View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
View SolutionConsider a spherical gaseous cloud of mass density rho(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If rho(r) is constant with time. the particle number density n(r)= rho(r) /m is : (G=universal gravitational constant)
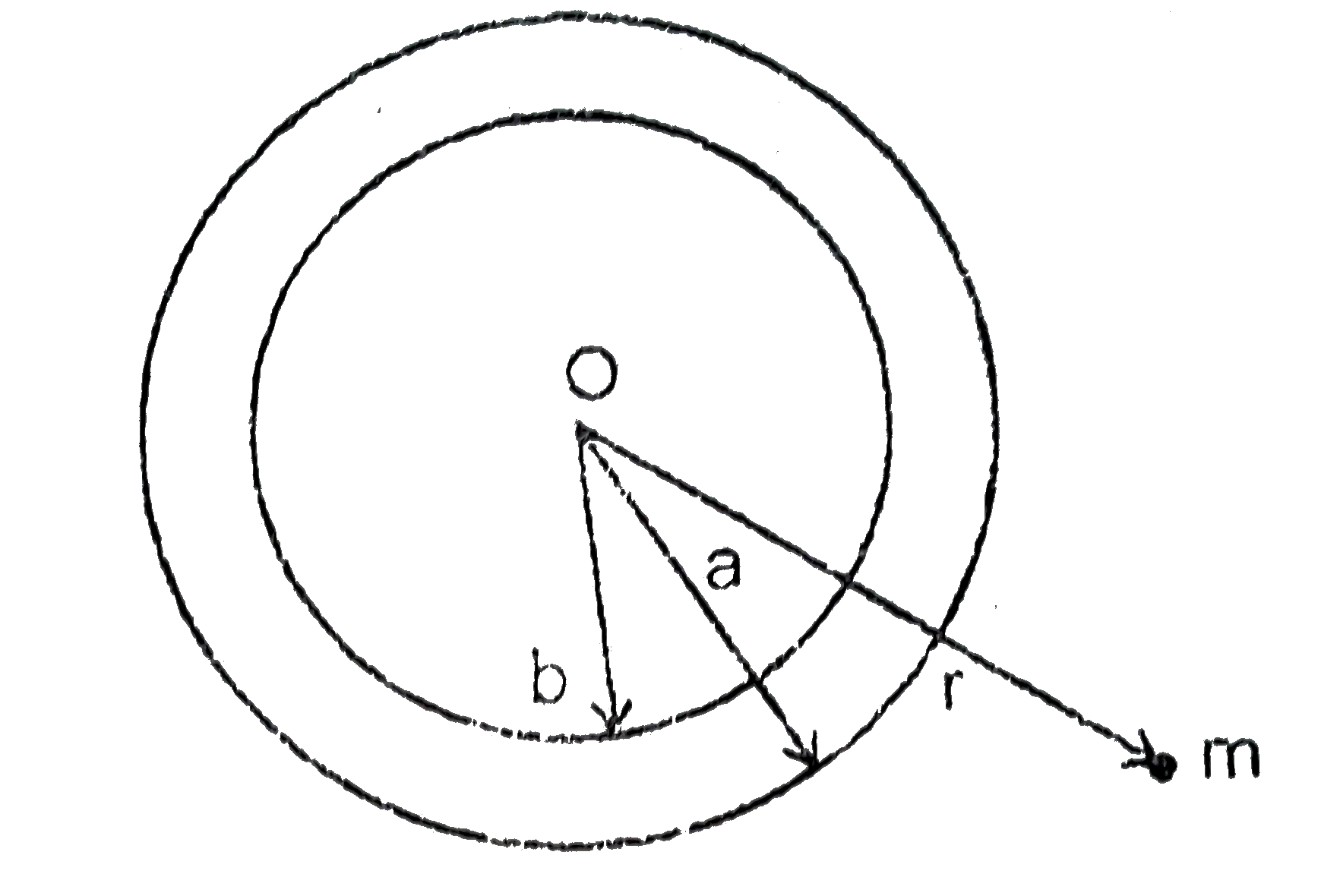
View SolutionA sphere of density rho and radius a has a concentric of radius b as shown in the (a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0 le r le oo (b) Sketch the corresponding curve for the potential energy u (r) of the system ,
View Solutionएक गोलाकार सममित (symmetrical) गुरुत्वीय के समूह का द्रव्यमान घनत्व ρ={ρ0r<R के लिए 0r>R के लिए }, जहाँ ρ0 एक अचल है |
समूह के केन्द्र r(0<r<∞) दूरी पर एक परीक्षण द्रव्यमान, कणो के गुरुत्वीय क्षेत्र के प्रभाव में वृत्तीय गति करता है | इसकी गति v को r के सापेक्ष किस प्रकार से दर्शाया जायेगा ?
View Solutionसमान द्रव्यमान M वाले चार कण पारस्परिक गुरूत्वीय बल के प्रभाव में R त्रिज्या के वृत्ताकार पथपर गतिशील है। प्रत्येक कण की चाल ज्ञात करें।
View Solutionएक परीक्षण कण, द्रव्यमान घनत्व ρ(r)=Kr2 से उत्पन्न गुरुत्वीय क्षेत्र में एक वृत्ताकार कक्षा में घूम रहा है। कण के कक्ष की त्रिज्या R तथा इसके आवर्तकाल T के बीच सही सम्बन्ध होगा
View SolutionThe mass density of a spherical body is given by ρ(r)=kr of r≤R where r is the distance r from the centre. The correct graph that describes qualitatively the acceleration, a, of . a test particle as a function of r is :
View Solutionएक गोलाकार सममित (symmetric) गुरूत्वीय कणों के समूह का द्रव्यमान घनत्व ρ={ρ0 for r≤R0 for r>R जहाँ ρ0 एक स्थिरांक है। कणों के गुरूत्वीय क्षेत्र के प्रभाव में एक परीक्षण आवेश वृत्तीय गति कर रहा है। निकाय के केन्द्र से r दूरी r(0<r<∞) पर इसकी चाल होगी।
View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionA spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
View SolutionA sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,
,
View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
View SolutionConsider a spherical gaseous cloud of mass density rho(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If rho(r) is constant with time. the particle number density n(r)= rho(r) /m is : (g =universal gravitational constant)
View Solution
