A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented bySolution in Marathi
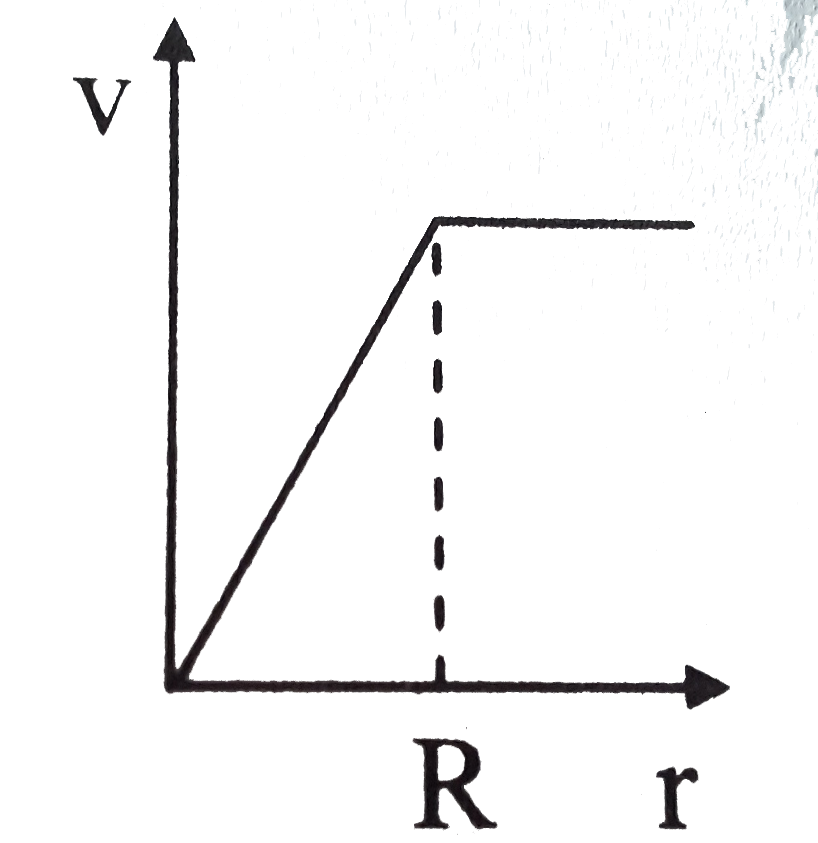
The correct Answer is:C
Step by step video & image solution for A spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} whererho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A spherically symmetric charge distribution is characterized by a charge density having the following variation : ρ(r)=ρ0forr<Rρ(r)=0 for r≥ R. Where r is the distance from the centre of the charge distribution and pois a constant. The electric field at an internal point (r
View Solutionएक गोलाकार सममित (symmetric) गुरूत्वीय कणों के समूह का द्रव्यमान घनत्व ρ={ρ0 for r≤R0 for r>R जहाँ ρ0 एक स्थिरांक है। कणों के गुरूत्वीय क्षेत्र के प्रभाव में एक परीक्षण आवेश वृत्तीय गति कर रहा है। निकाय के केन्द्र से r दूरी r(0<r<∞) पर इसकी चाल होगी।
03:27View SolutionA spherically symmetric charge distribution is characterized by a charge density having the following variation : rho (r ) = rho_0 (1 - r/R) for r lt R rho (r ) = 0 for r ge R . Where r is the distance from the centre of the charge distribution and rho_0 is a constant. The electric field at an internal point (r lt R) is
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
03:09View SolutionA spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
03:00View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
02:57View SolutionA spherically symmetric gravitational system of particles has a mass density where r_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed V as a function of distance r (0 lt r lt oo) from the centre of the system is represented by
03:38View Solution

