The two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
8
10
12
14
The correct Answer is:D
To find the length of chord AB in the circle where the two chords AB and CD intersect at point P, we can use the property of intersecting chords. The property states that if two chords intersect each other, the products of the lengths of the segments of each chord are equal.
Let's denote:
- BP = 4 cm
- PD = 5 cm
- CP = 8 cm
- AP = x cm (this is what we need to find)
According to the intersecting chord theorem:
AP×BP=CP×PD
Step 1: Write the equation based on the intersecting chords theorem
Using the values we have:
x×4=8×5
Step 2: Calculate the right side of the equation
Calculating the right side:
8×5=40
So, we have:
4x=40
Step 3: Solve for x
Now, divide both sides by 4:
x=404=10
Thus, AP = 10 cm.
Step 4: Find the length of chord AB
Now that we have AP, we can find the length of chord AB:
AB=AP+PB
Substituting the known values:
AB=10+4=14 cm
Final Answer
The length of chord AB is 14 cm.
---
- BP = 4 cm
- PD = 5 cm
- CP = 8 cm
- AP = x cm (this is what we need to find)
AP×BP=CP×PD
Using the values we have:
x×4=8×5
Calculating the right side:
8×5=40
So, we have:
4x=40
Now, divide both sides by 4:
x=404=10
Thus, AP = 10 cm.
Now that we have AP, we can find the length of chord AB:
AB=AP+PB
Substituting the known values:
AB=10+4=14 cm
The length of chord AB is 14 cm.
Similar Questions
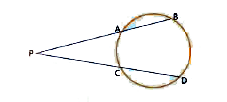
In the given figure,chords AB and CD of a circle intersect externally at P. AB=4 cm,CD=11 cm and PD=15 cm,then the length of PB is:
 View Solution
View SolutionIn the figure, chords AB and CD of a circle intersect externally at P. If AB = 4cm, CD =11cm and PD=15cm, then the length of PB is:
दी गयी आकृति में, जीवा AB और CD एक वृत्त को बाहरी रूप से P पर काटते हैं। यदि AB = 4cm, CD =11 cm और PD = 15cm है, तो PB की लंबाई ज्ञात करे | View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Chords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
A5 cmB7.35 cmC6 cmD4 cm - Question 2 - Select One
Two mutually perpendicular chords AB and CD intersect at point P inside the circle such that CP=15cm.,PD=8cmandPB=6cm. Find the length AC (in cm.)
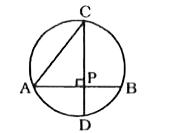 A25B24C20D18
A25B24C20D18 - Question 3 - Select One
If AB and CD are two chords of a circle intersected at point O. If CO = 4cm and OD = 3.5 cm and AB = 9 cm then find the length of smaller between AO and BO.
A3 cmB2 cmC4 cmD6 cm
Chords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is :
एक वृत्त की जीवायें AB और CD एक दूसरे को बाहर से P पर काटती हैं | यदि AB = 6 सेमी,CD =3 सेमी और PB =4 सेमी है, तो PD की लंबाई (सेमी में ) ज्ञात करें |View SolutionChords AB and CD of a circle Intersect at E. If AE = 9 cm, BE = 12 cm and CE = 3DE, then the length of DE (in cm) is
View SolutionThe chords AB and CD of a circle intersect at E. If AE = 12cm, BE = 20.25 cm and CE = 3DE, then the length (in cm) of CE is:
एक वृत्त की दो जीवाएँ AB तथा CD एक-दूसरे को E पर काटती हैं | यदि AE = 12 सेमी, BE =20.25 सेमी तथा CE = 3DE है, तो CE की लंबाई ( सेमी में ) कितनी होगी ?View SolutionA circle with radius 12 cm has two perpendicular chords AB and CD intersecting at a point R, other than the centre O, where RD=6cm and RB=18cm. Find the length of AR.
View SolutionTwo chords AB and CD of a circle intersect each other at P internally. If AP = 3.5 cm, PC = 5 cm, and DP = 7 cm, then what is the measure of PB?
View Solution

