A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Find sum of the areas of all squares as n tends to infinitySolution in Bengali
Step by step video & image solution for A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times. Find sum of the areas of all squares as n tends to infinity by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionFind the area of the figure enclosed by the curve 5x2+6xy+2y2+7x+6y+6=0.
View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionIn a circle of radius R a square is inscribed, then a circle is inscribed in the square,a new square in the circle and so on for n xx.If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas of all the squares as n rarr oo is k, then find the value of (4k)/(pi) .
View SolutionA square ABCD is inscribed in a circle of radius r. Find the area of the square.
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View SolutionA square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is
View SolutionA circle is inscribed ina n equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .

What is the radius of the inner - most circle ?
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
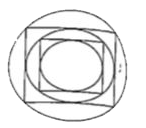
What is the sum of areas of all the squares shown in the figure ?
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
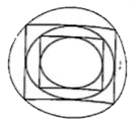
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?
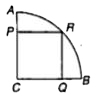
View SolutionIn the adjoining figure a quadrant ( of circle ) inscribes a square of maximum possible area . If the radius of the circle be 'r' then what is the area of the square ?
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View Solution
