In a triangle ABC, right angled at A, on the leg AC as diameter, semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals toSolution in Bengali
Step by step video & image solution for In a triangle ABC, right angled at A, on the leg AC as diameter, semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionIn a right triangle ABC ,right angled at A, on the leg AC as diameter,a semicircle is described.The chord joining A with the point of intersection D of the hypotenuse and the semicircle,then the length AC equals to
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
View SolutionLet ABC be a right triangle with length of side AB=3 and hypotenuse AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter,a semicircle is described.If a chord joi A with the point of intersection D of the hypotenuse and the semicircle,then the length of AC equals to
View SolutionABC is a right angle in a right triangle ABC. If the line drawn parallel to BC through the hypotenuse AB denominator M intersects AC at D, then prove the following point AC midpoint D
View Solution∠ACB is an angle in the semicircle of diameter AB =5 and AC : BC = 3 : 4 The area of the triangle ABC is
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View Solutionangle A At right angles Delta ABC Assuming the side AC of the diameter to be drawn, a semicircle is drawn. If a chord connects the point and the intersection of the hypotenuse and the semicircle of the triangle, then the length of the side AC is
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View Solutionएक समकोण त्रिभुज ABC के कर्ण AC का मध्य बिन्दु D है तो सिद्ध करें कि BD=12AC

View SolutionABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : D is the midpoint of AC.
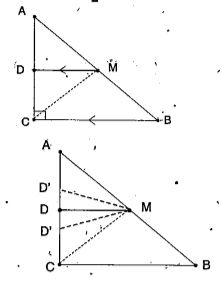
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals to
View Solution
