In a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joi A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals to
Step by step video & image solution for In a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joi A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
View SolutionIn a right triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. The chord joining A with the point of intersection D of the hypotenuse and the semicircle, then the length AC equals to
View SolutionA right angle triangle whose hypotenuse is c and its perpendicular sides are a and b. Three semicircles are drawn along the three sides of this triangle in such a way that the diameter of each semicircle is equal to the length of the respective side of the triangle. The semicircle drawn wiht the help of hypotenuse intersects the other two semicircles as shown in the concerned diagram. Find the area of the shaded region.
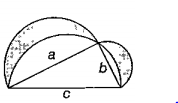
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View SolutionIn a right -angle triangle, the length of the sides containing the right angles area aandb. With the mid-point of each sides as centres three semicircles are drawn outiside the triangle. Find the area of Δ and the semicircles together
View SolutionIn a right -angle triangle, the length of the sides containing the right angles are aandb. With the mid-point of each sides as centres three semicircles are drawn outiside the triangle. Find the area of Δ and the semicircles together
View SolutionIn a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionIn a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View Solution
