Let C1andC2 be, respectively, the parabola x2=y−1andy2=x−1.
Also, let P any point on C1andQ be any point on C2. If P1andQ1 are the reflections of P and Q, respectively, with respect to the line y=x, then Solution in Bengali
Step by step video & image solution for Let C_(1)andC_(2) be, respectively, the parabola x^(2)=y-1andy^(2)=x-1. Also, let P any point on C_(1)andQ be any point on C_(2). If P_(1)andQ_(1) are the reflections of P and Q, respectively, with respect to the line y=x, then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionThe circle C1:x2+y2=3, with centre at O, intersects the parabola x2=2y at the point P in the quadrant. Let the tangent to the circle C1 at P touches other tqo circles C2andC3 at R2andR3, respectively. Suppose C2andC3 have equal radii 2√3 and centres Q2andQ3. respectively. If Q2andQ3 lie on the y-axis, then
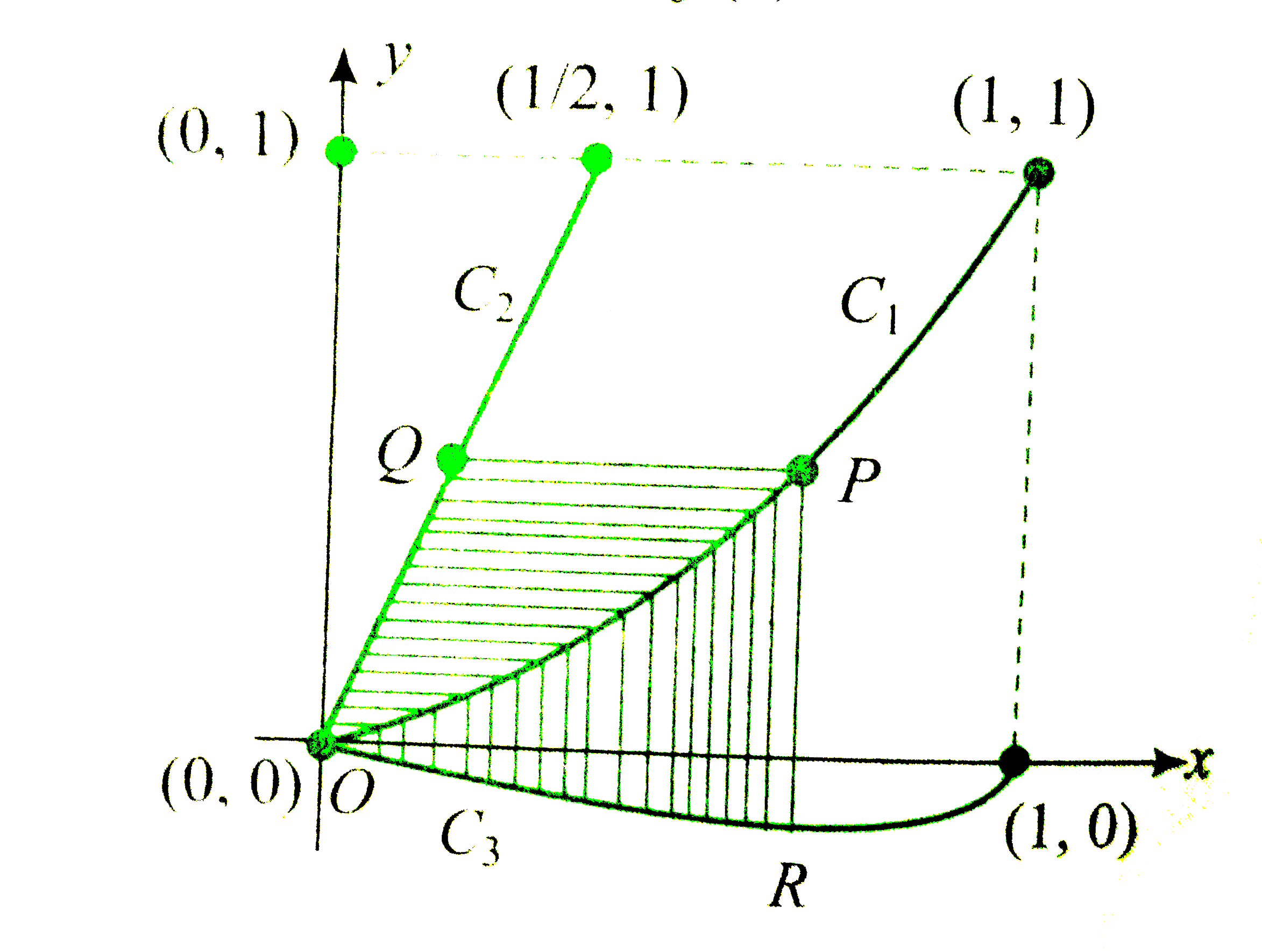
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the line
View SolutionLet E be the ellipse x^(2)/9 + y^(2)/4 = 1 and C be the circle x^(2) + y^(2) = 9. Let P and Q be the points (1, 2) and (2, 1) respectively. Then,
View SolutionLet C1 and C2 be respectively, the parabolas x2=y=−1 and y2=x−1 Let P be any point on C1 and Q be any point on C2 . Let P1 and Q1 be the refelections of P and Q, respectively with respect to the line y=x.
If the point p(π,π2+1) and Q(π2+1μ) then P1 and Q1 are
View SolutionLet C1 and C2 denote the centres of the circles x2+y2=4 and (x−2)2+y2=1 respectively and let P and Q be their points of intersection. Then the areas of triangles C1PQ and C2PQ are in the ratio _
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View SolutionLet E be the ellipse x^(2)//9+y^(2)//4=1 and C be the circle x^(2)+y^(2)=9 . Let P and Q be the points (1, 2) and (2, 1) respectively. Then
View Solutionमाना C1 व C2 क्रमश: परवलय x2=y−1 और y2=x−1 हैं। माना P,C1 पर तथा Q,C2 पर कोई बिन्दु है। माना P और Q, रेखा y= x के सापेक्ष क्रमश: P और Q के प्रतिबिम्ब हैं। सिद्ध कीजिए कि P1,C2, पर तथा Q1,C1 पर स्थित हैं और PQ≥ min{PP1,Q1} अत: या अन्यथा C1 और C2 पर क्रमश: बिन्दु P0 और Q0 इस प्रकार जात कीजिए, कि सभी बिंदु युग्म (P,Q) के लिए P0Q0≤PQ जहाँ P,C1 पर और Q,C2 पर है।
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View Solutionमाना कि C1 और C2 दो वृत्तों क्रमश: x2+y2=4 और (x−2)2+y2=1 के केन्द्र को प्रदर्शित करते हैं और माना कि P और Q दोनों के प्रतिच्छेदन बिन्दु है तब त्रिभुजों C1PQ और C2PQ के क्षेत्रफलों का अनुपात है
View SolutionLet C1 and C2 be respectively, the parabolas x2=y−1 and y2=x−1 Let P be any point on C1 and Q be any point on C2 . Let P1 and Q1 be the refelections of P and Q, respectively with respect to the line y=x.
If the point p(π,π2+1) and Q(μ2+1,μ) then P1 and Q1 are
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The co-ordinates of P1 are :
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View Solution
