If the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3is,θ then the find the value of cosecθ.Solution in Bengali
The correct Answer is:2
Vector normal to the plane is →n=ˆi−3ˆj+2ˆk and vector along the line is →v=2ˆi+ˆj−3ˆk
Now sinθ=→x⋅→v|→x||→v|=∣∣
∣∣2−3−6sqr(14)√14∣∣
∣∣=∣∣∣714∣∣∣
Hence, cosecθ=2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SUBJECTIVE TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SINGLE CORRECT ANSWER TYPE9videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Find the equation of the plane passing through the points (2,1,0),(5,0,1) and (4,1,1).
03:45View SolutionThe value of k such that x−41=y−21=z−k2 lies in the plane 2x−4y=z=7 is a. 7 b. -7 c. no real value d. 4
05:28View Solution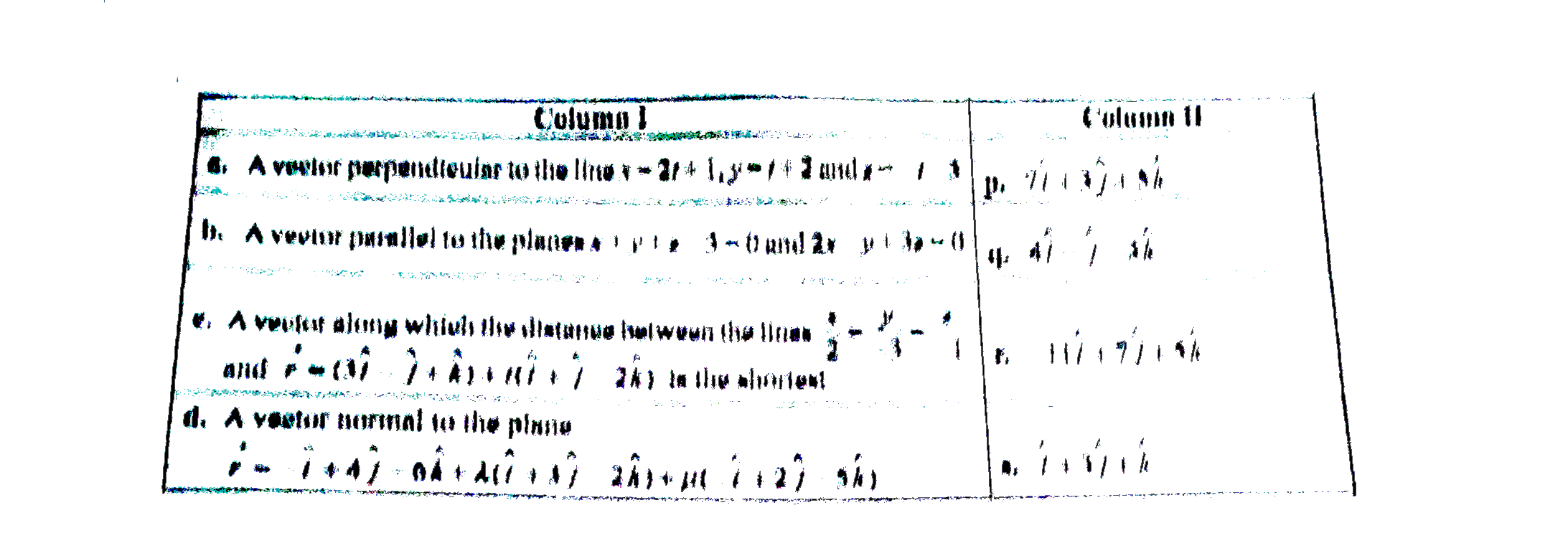
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
07:02View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
02:32View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3isθ, then the find the value of cosecθ.
03:43View SolutionStatement 1: Let θ be the angle between the line x−22=y−1−3=z+2−2 and the plane x+y−z=5. Then θ=sin−1(1/√51). Statement 2: The angle between a straight line and a plane is the complement of the angle between the line and the normal to the plane.
11:21View SolutionIf the angle between the line x−11=y−2k=z+34 and the plane x-3y+2z+5=0 is sin−1(37√6), the value of k is
04:34View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−1−1=z−1−3 is θ, then sec2θ is equal to
View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3is,θ then the find the value of cosecθ.
04:31View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3 is θ, then the find the value of cosecθ.
03:11View SolutionIf the angle between the line x−11=y−2k=z+34 and
the plane x−3y+2z+5=0 is sin−1(37√6), the value of k is04:13View SolutionFind the angle between the plane x+y+z−2=0 and line x+32=y−11=z+14
02:10View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3 is θ, then the value of cosecθ is
05:37View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−1−1=z−1−3 is θ, then sec2θ is equal to
06:27View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3isθ, then the find the value of cosecθ.
02:31View Solution