If (a,b,c) is a point on the plane 3x+2y+z=7, then find the least value of 2(a2+b2+c2), using vector method.Solution in Bengali
The correct Answer is:7
Clearly minimum value of a2+b2+c2
=⎛⎜
⎜⎝|(3(0)+2(0)+(0)−7)|√(3)2+(2)2+(1)2⎞⎟
⎟⎠2=4914=72 units
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SUBJECTIVE TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SINGLE CORRECT ANSWER TYPE9videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Find the equation of the plane passing through the points (2,1,0),(5,0,1) and (4,1,1).
02:21View SolutionThe value of k such that x−41=y−21=z−k2 lies in the plane 2x−4y=z=7 is a. 7 b. -7 c. no real value d. 4
02:10View Solution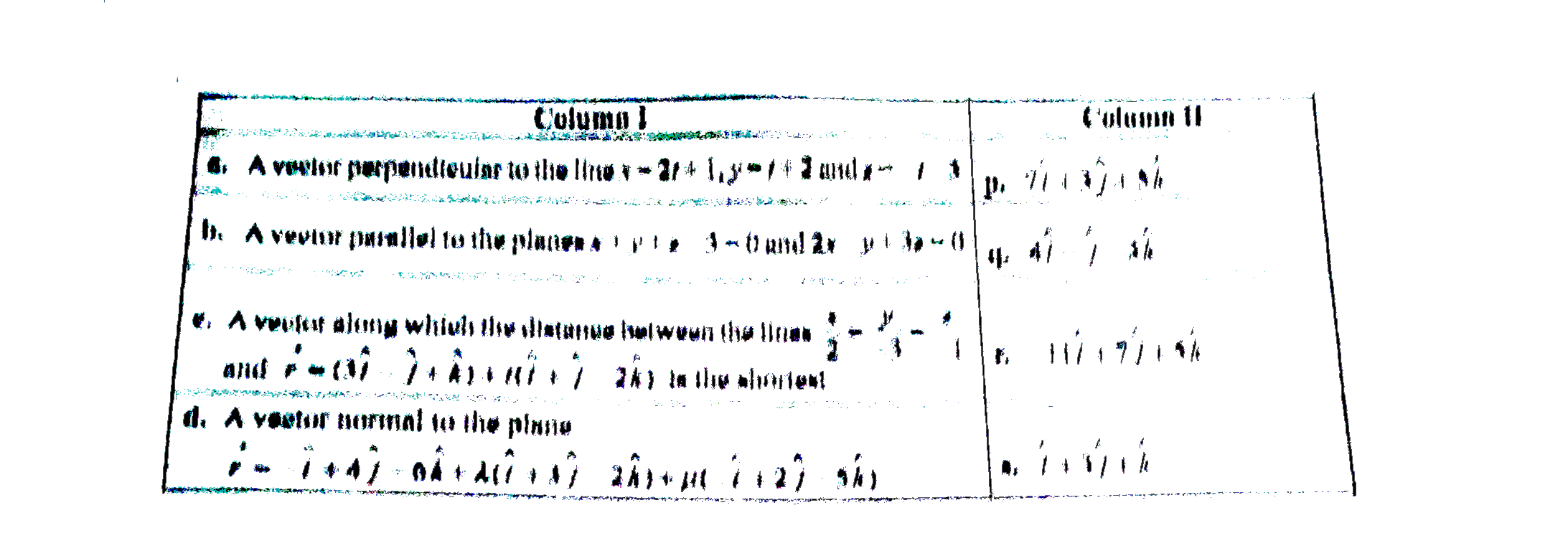
02:48View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
02:30View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
04:47View SolutionIf (a,b,c) is a point on the plane 3x+2y+z=7, then find the least value ofvector method.a^(2)+b^(2)+c^(2), using vector method.
01:26View SolutionA=2x+3xy+7x2,B=3x−2xy−5x2andC=2xy−6x2−3x. Find the value of A+B-C.
03:03View SolutionUsing the vector method , find the values of λ and μ for which the points
A(3,λ,μ)B(2,0,−2) and C(1,−2,−5) are collinear04:01View SolutionLet P(a,b,c) be any on the plane 3x+2y+z=7, then find the least value of 2(a2+b2+c2).
04:29View SolutionIf a,b and c are vectors with magnitudes 2,3 and 4 respectively then the least upper bound of |a−b|2+|b−c|2+|c−a|2 among the given values is
01:26View SolutionIf (a,b,c) is a point on the plane 3x+2y+z=7, then find the least value of 2(a2+b2+c2), using vector method.
02:33View SolutionIf (a,b,c) is a point on the plane 3x+2y+z=7, then find the least value of a2+b2+c2, using vector method.
02:30View SolutionUsing vector method, prove that the following points are collinear:
A(6,-7,-1) B(2,-3,1) C(4,-5,0)03:19View SolutionUsing vector method prove that the points A(6,−7,−1),B(2,−3,1) and C(4,−5,0) are collinear.
02:26View SolutionIf (a,b,c) is a point on the plane 3x+2y+z=7, then find the least value of 2(a2+b2+c2), using vector method.
03:24View SolutionIfA= 2y^2 + 3x- x^2 ,B = 3 x^2 - y^2 and C =5 x^2 -3xy then find B+C
06:34View Solution