In how many ways three letters a,b,c can be arranged without repetition ?Solution in Bengali
The correct Answer is:C
A plane containing the line of intersection of the given planes is
x−y−z−4+λ(x+y+2z−4)=0
i.e., (λ+1)x+(λ−1)y+(2λ−1)z−4(λ+1)=0
vector normal to it
V=(λ+1)ˆi+(λ−1)ˆj+(2λ−1)ˆkS (i)
Now the vector along the line of intersection of the planes 2x+3y+z−1=0andx+3y+2z−2=0 is given by
→n=∣∣
∣
∣∣ˆiˆjˆk231132∣∣
∣
∣∣=3(ˆi−ˆj+ˆk)
As →n is parallel to the plane (i), we have
→n⋅→V=0
(λ+1)−(λ−1)+(2λ−1)=0
2+2λ−1=0orλ=−12
Hence, the required plane is
x2−3y2−2z−2=0
x−3y−4z−4=0
Hence, |A+B+C|=6
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SUBJECTIVE TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SINGLE CORRECT ANSWER TYPE9videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Find the equation of the plane passing through the points (2,1,0),(5,0,1) and (4,1,1).
02:13View SolutionThe value of k such that x−41=y−21=z−k2 lies in the plane 2x−4y=z=7 is a. 7 b. -7 c. no real value d. 4
01:17View Solution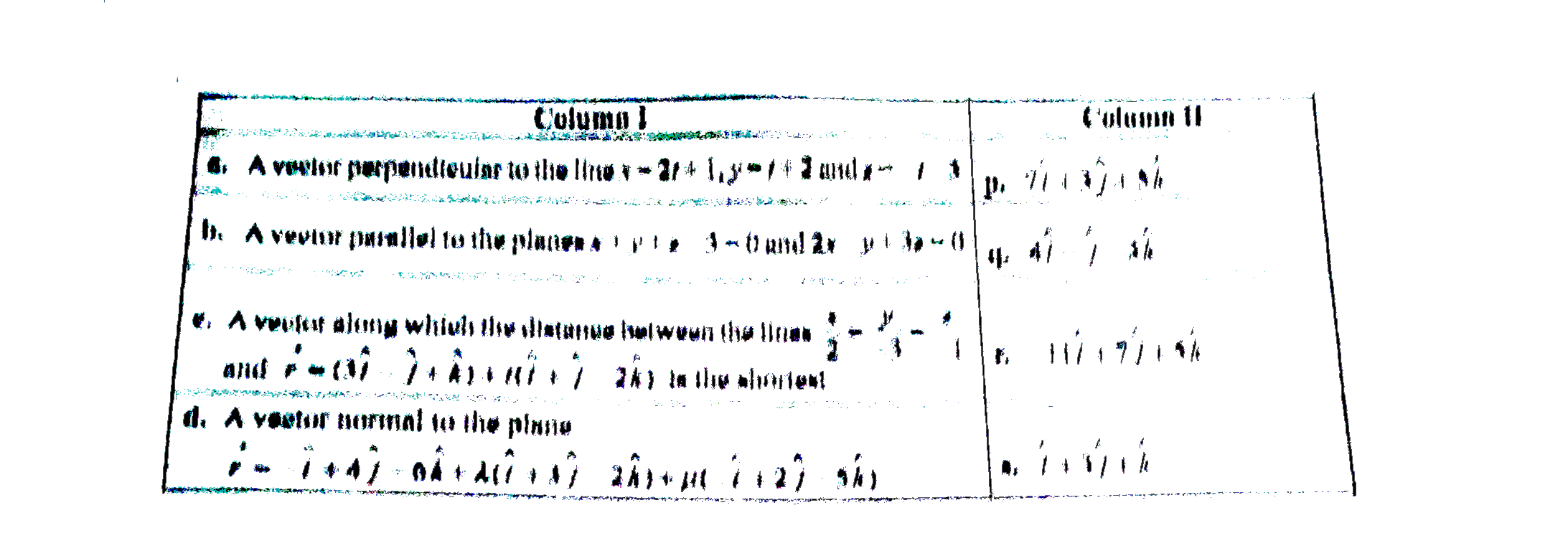
01:41View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
01:14View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
01:16View SolutionHow many 4-letter word, with or without meaning, can be formed out of the letters of the word, ‘LOGARITHMS’, if repetition of letters is not allowed?
01:52View SolutionIn how many ways can the letters of the word ARRANGE' be arranged
04:03View SolutionHow many three letter words can be formed using a,b,c,d,e if Repetition is not allowed ii. repetition is allowed?
01:31View SolutionHow many 5-letter words, with or without meaning, can be formed out of the letters of the word EQUATIONS if repetition of letters is not allowed ?
02:05View SolutionHow many 3-letter words can be formed using a, b, c, d, e if
(i) repetition of letters is not allowed?
(ii) repetition of letters is allowed?05:59View SolutionHow many 4-letter words, with or without meaning, can be formed out of the letters in the word LOGARITHMS, if repetition of letters is not allowed ?
01:57View SolutionIn how many ways the letters of the word “ARRANGE” can be arranged without altering the relative positions of vowels & consonants ?
04:03View Solutionतीन अक्षरों a,b,c को कितने भिन्न प्रकार से लिख सकते हैं?
03:25View SolutionHow many 4-letter words, with or without meaning, can be formed out of the letters in the word LOGARITHMS, if repetition of letters is not allowed ?
03:20View SolutionHow many 4-letter word, with or without meaning, can be formed out of the letters of the word, ‘LOGARITHMS’, if repetition of letters is not allowed?
02:00View Solution