The angle of elevation of the top of a tower a point A due south of it is 30∘ and from a point B due west of it is 45∘ .If the height of the tower is 100 meters ,then find the distance AB.Solution in Bengali
In the following figure OP is the tower .
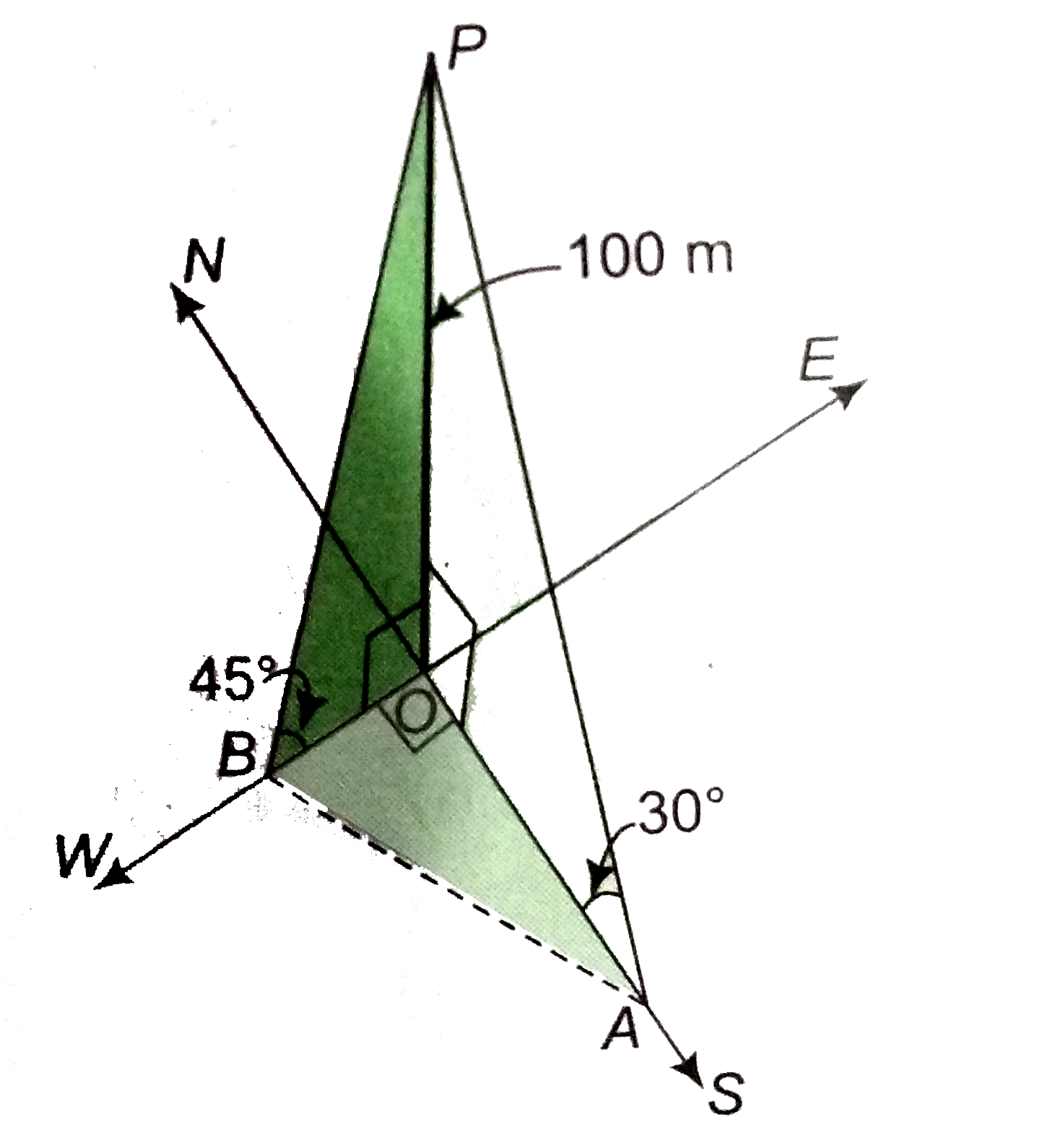
Op= 100 m
In right angled triangle :POA ,
tan30∘=100OA
∴OA=100cot30∘=100√3
In right angled triangle POB,
tan45∘=100OB
∴OB=100cot45∘=100
In right angled triangle AOB, using Pythagoras theorem ,we get
AB2=OA2+OB2
=3×1002+1002
=4×1002
∴AB=2×100=200m
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Exercises18videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
02:02View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
02:58View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
05:57View SolutionFrom a point A due North of a tower,the angle of elevation of the top of the tower is 30^(@). From a point B due South,the elevation is 45^(@). If AB=100 metres,find the height of the tower
02:26View SolutionAngle of elevation of top of a tower from a point 'A' due E30∘N of tower on the ground is 45∘. While angle of elevation of top of tower from a point 'B' due N60∘W of tower is 30∘ where AB=50 m, then height of tower is
05:03View Solutionएक मीनार के पाद से 40 मीटर दुरी पर स्तिथित किसी बिनु से मीनार के शिखर का उनयन कोण 30∘ है मीनार की उचाई ज्ञात कीजिएः
05:01View SolutionThe angular elevation of a tower OP at a point A due south of it is 60∘ and at a point B due west of A, the elevation is 30∘. If AB=3m, the height of the tower is
04:04View SolutionThe angle of elevation of the top of a vertical tower from a point A due east of it is 45∘. The angle of elevation of the top of the same tower from a point B due south of A is 30∘. If the distance between A and B is 54√2 m then the height of the tower (in metres), is
07:59View SolutionThe angular elevations of a tower CD at a place A due south of it is 60∘ , and at a place B due west of A, the elevation is 30∘ . If AB=300m, what is the height, in meters, of the tower?
04:13View SolutionThe angle of elevation of the top of a tower at a point A due south of the tower is α and at β due east of the tower is β. If AB=d, then height of the tower is
03:50View SolutionThe elevation of a tower at a station A due north of it is 45∘ and at a station B due west of A is 30∘.
If AB=40 m, find the height of the tower:07:20View SolutionAngle of elevation of the top of the tower from station A to the west of a tower 45^(@) is. Station B, located 10 meters from A, to the south of the east of the tower 45^(@) Angle of elevation of the top of the tower from 30^(@) Is the height of the tower
07:20View Solutionएक मीनार के दक्षिण की ओर बिन्दु A पर मीनार का उन्नयन कोण 45∘ तथा उत्तर की ओर स्थित बिन्दु B पर मीनार का उन्नयन कोण 45∘ हैं यदि मीनार की ऊँचाई 100 मीटर हो तो AB=
04:38View SolutionThe angle of elevation of the top of the top of a vertical tower from a point A, due east of it is 45∘. The angle of elevation of the top of the same tower from a point B, due south of A is 30∘. If the distance between A and B is 54√2m, then the height of the tower (in meters), is
05:56View SolutionThe angle of elevation of a top of a tower from a point A due south of it tan−1 (6) and that from B due to west of it is tan−1 (7.5). If h is the height of the tower AB=λh then λ2=
View Solution

