Draw the graph of $y = \tan^{- 1} (\frac{3 x - x^{3}}{1 - 3 x^{2}})$ .Solution in Bengali

Video Solution

Text Solution

Verified by Experts

We have $y = f (x) = \frac{3 x - x^{3}}{1 - 3 x^{2}}$ , which is an odd function.
Domain of the function is $R - {\pm \frac{1}{\sqrt{3}}}$
1. y-intercept
f(0)=0
So the graph cuts the y-axis at (0,0).
2. x-intercept (zeros)
Put y=0 or $3 x - x^{3} = 0 ∴ x = 0, \pm \sqrt{3}$
So the graph meets the x-axis at (0,0) and $(\pm \sqrt{3}, 0)$ .
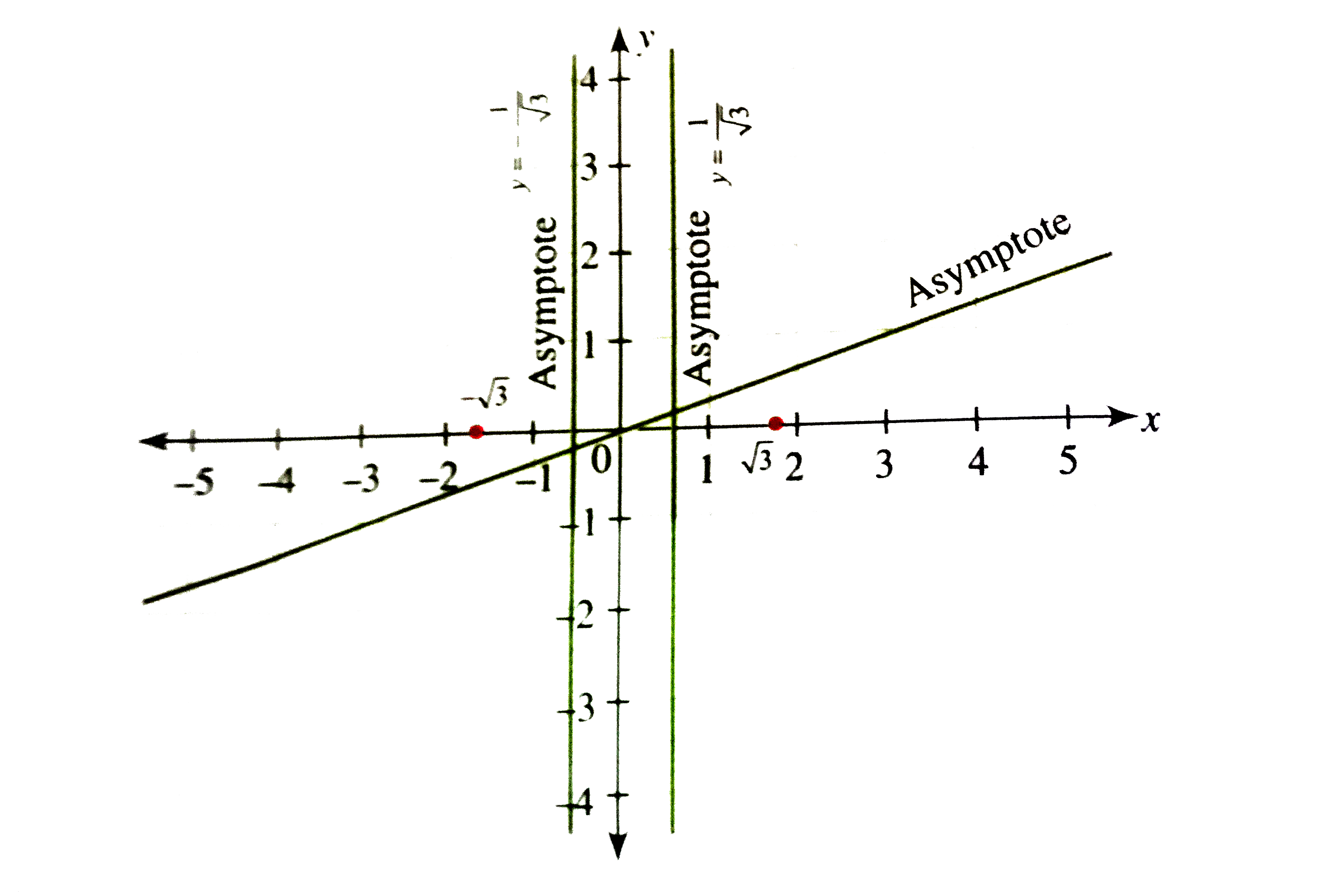
3. Asymptotes
Vertical asymptotes
Clearly , the graph has vertical asymptote $x = \pm \frac{1}{\sqrt{3}}$ , where the denominator becomes zero.
Horizontal asymptotes
Clearly, the graph has no horizontal asymptote as the degree of the numerator is higher than the degree of the numerator is higher than the degree of the denominator.
Oblique asymptotes ltbr> $y = \frac{x^{3} - 3 x}{3 x^{2} - 1} = \frac{1}{3} x - \frac{- \frac{8}{9} x}{3 x^{2} - 1}$
Hence the oblique asymptote is $y = \frac{1}{3} x$ .
Thus, important points ans lines are as shown in the following figure.

4. Monotinicity/Extremum
$f' (x) = \frac{(3 - 3 x^{2}) (1 - 3 x^{2}) + 6 x (3 x - x^{3})}{{(1 - 3 x^{2})}^{2}}$
$= 3 \frac{{(x^{2} + 1)}^{2}}{{(1 - 3 x^{2})}^{2}} > 0$
Hence the function is increasing throughout.
$lim_{x \to - \frac{1^{-}}{\sqrt{3}}} \frac{3 x - x^{3}}{1 - 3 x^{2}} = \infty$ and $lim_{x \to - \frac{1^{+}}{\sqrt{3}}} \frac{3 x - x^{3}}{1 - 3 x^{2}} = - \infty$
f(x) approaches asymptote $y = x / 3$ as $x \to - \infty$ .
Thus, in $(- \infty, - \frac{1}{\sqrt{3}})$ , f(x) increases from $' - \infty'$ to $' \infty'$ intersecting the x-axis at $(- \sqrt{3}, 0)$
$lim_{x \to - \frac{1^{+}}{\sqrt{3}}} \frac{3 x - x^{3}}{1 - 3 x^{2}} = - \infty$ and $lim_{x \to {\sqrt{3}}^{-}} \frac{3 x - x^{3}}{1 - 3 x^{2}} = \infty$
Thus, in $(- \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$ , f(x) increases from $' - \infty'$ to $' \infty'$ intersecting the x-axis at (0,0).
$lim_{x \to {\sqrt{3}}^{+}} \frac{3 x - x^{3}}{1 - 3 x^{2}} = - \infty$ and $lim_{x \to \infty} \frac{3 x - x^{3}}{1 - 3 x^{2}} = \infty$
Thus, in $(\frac{1}{\sqrt{3}}, \infty), f (x)$ increases from $' - \infty'$ to $' \infty'$ intersecting the x-axis at $(\sqrt{3}, 0)$ .
f(x) approaches asymptote $y = x / 3$ as $x \to \infty$ .
From the above discussion, the graph of $y = f (x)$ can be drawn as follows.

Now in each of the intervals $(- \infty, - \frac{1}{\sqrt{3}}), (- \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}), (\frac{1}{\sqrt{3}}, \infty), f (x)$ takes values $(- \infty, \infty)$ .
So in each of the intervals, $\tan^{- 1} . \frac{3 x - x^{3}}{1 - 3 x^{2}}$ takes values $(- \frac{π}{2}, \frac{π}{2})$ .
So the graph of $g (x) = \tan^{- 1} . \frac{3 x - x^{3}}{1 - 3 x^{2}}$ can be drawn as follows.

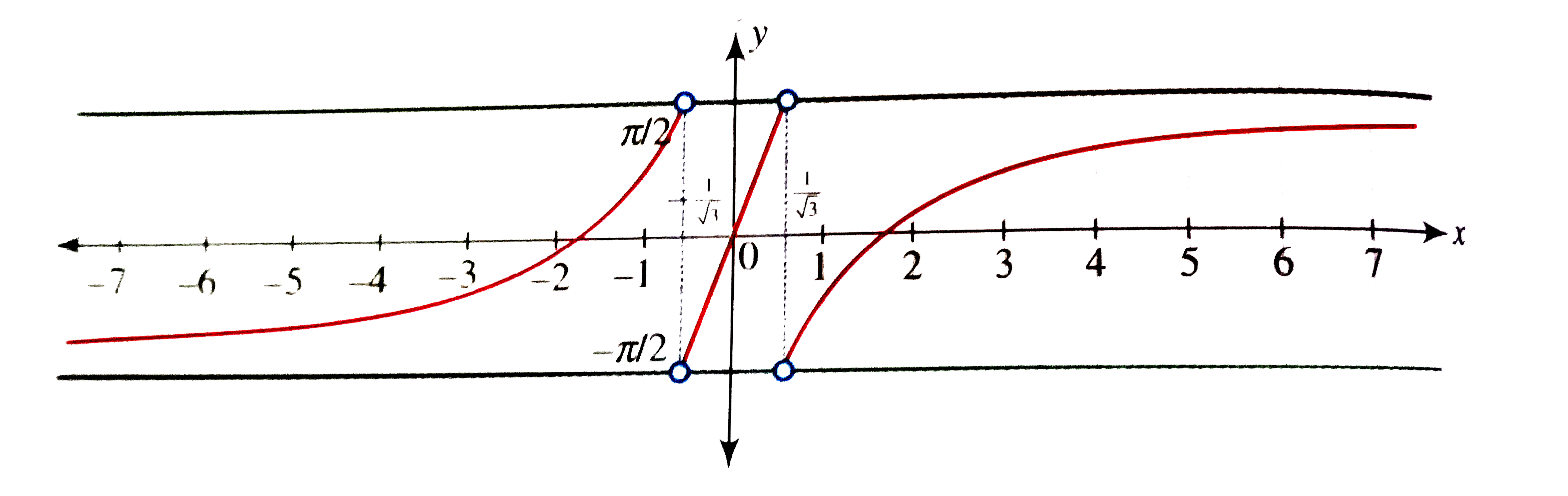
Here $y = \pm \frac{π}{2}$ are asymptotes.

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS-Exercises

Home
Ask Doubt
Profile