Let f(x+y2)=f(x)+f(y)2 for all real x and y. If f'(0) exists and equals-1 and f(0)=1, find f(2) Solution in Bengali
Suppose A(x,f(x))andB(y,f(y)) be any two points on the curve y=f(x).
If M is the mid-point of AB, then the coordinates of M are (x+y2,f(x)+f(y)2).
Now the foot of the perpendicular from the M on the x-axis is L. ML meets the curve y=f(x) at P.
According to the graph, the coordinates of P are (x+y2,f(x+y2))andPL>ML.
⇒ f(x+y2)>f(x)+f(y)2
But given f(x+y2)=f(x)+f(y)2, which is possible when P→M.
That is, P lies on AB. Hence y=f(x) must be a linear function.
Let f(x)=ax+b ⇒f(0)=0+b=1 (given )
and f'(x)=a ⇒f'(0)=a=−1 (given )
∴ f(x)=−x+1
∴ f(2)=−2+1=−1
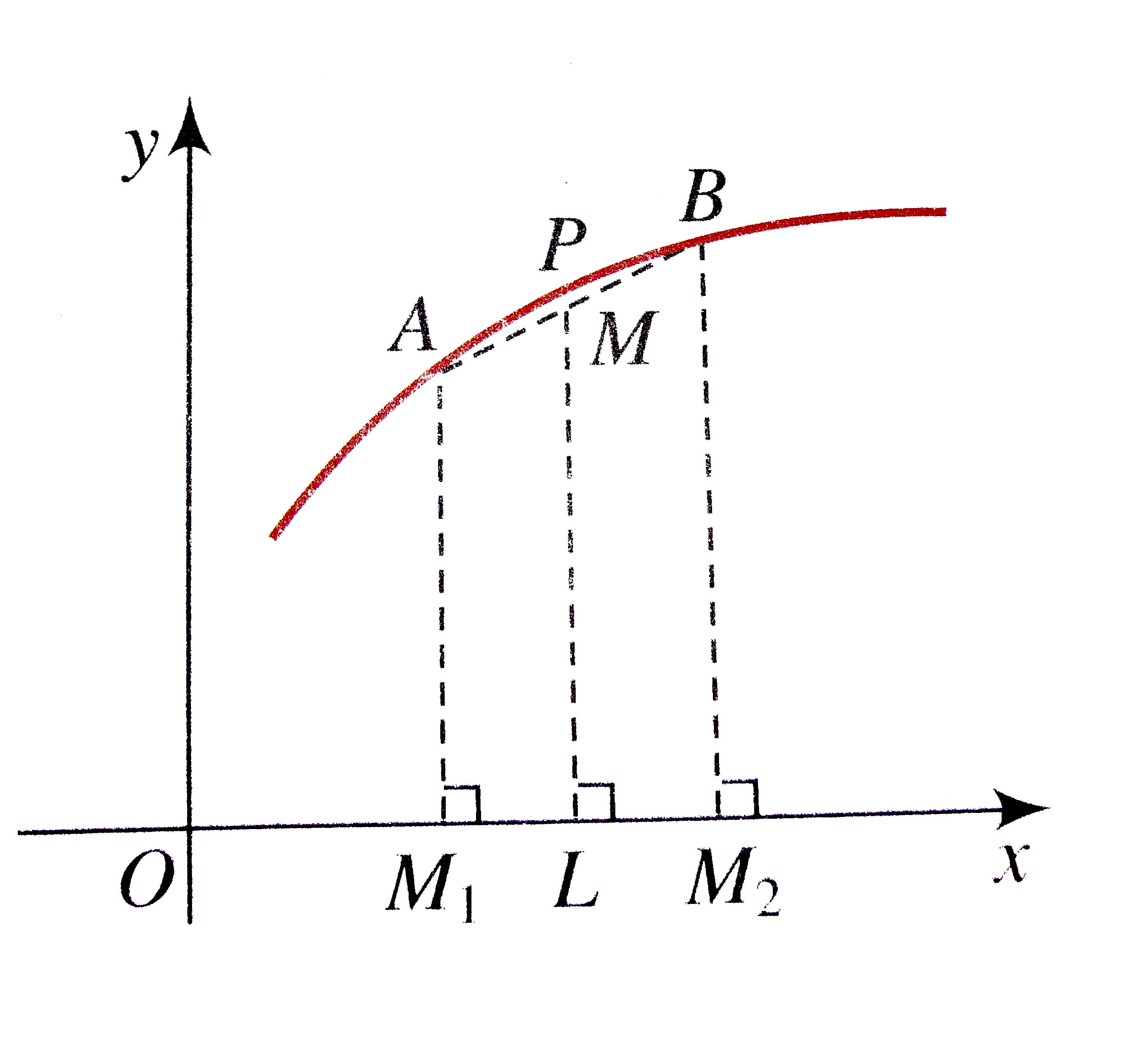
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
03:55View SolutionDraw the graph of y=(x−1)(x2−x+1).
06:51View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
07:06View SolutionLet f(x+y2)=f(x)+f(y)2forallrealxandy If f′(0) exists and equals −1andf(0)=1,thenf∈df(2).
02:19View SolutionLet f((x+y)/(2))=(f(x)+f(y))/(2) for all real x and y.If f(0) exists and equals-1and f(0)=1 find f(2)
06:29View SolutionLet f(x+y)=f(x)+f(y) for all real x,y and f'(0) exists.Prove that f'(x)=f'(0) for all x in R and 2f(x)=xf(2)
03:49View SolutionLet f(x) be a real valued function such that f(0)=12 and f(x+y)=f(x)f(a-y)+f(y)f(a-x),∀x,y∈R, then for some real a,
07:23View SolutionLet f(x+y2)=12|f(x)+f(y)|for all real x and y, if f'(0) exists and equal to (−1),andf(0)=1 then f(2) is equal to-
05:38View SolutionIf f(x+y)=f(x)⋅f(y) for all real x and y and f(5)=2,f'(0)=3, find f'(5).
06:07View SolutionLet f(x+y2)=12[f(x)+f(y)] for all real x and y. If f'(0) exists and equals (−1),f(0)=1, find f(2).
03:45View Solutionमाना f[(x+y)2]={f(x)+f(y)2}, सभी वास्तविक x और y के लिए, यदि f'(0) का अस्तित्व है तथा '-1' के बराबर है और f(0) = 1, तब f(2) ज्ञात कीजिए |
12:44View Solutionমনে করো, x ও y-এর সব বাস্তব মানে, f(x+y2)=12[f(x)+f(y)], যদি f'(0) -এর অস্তিত্ব থাকে এবং f'(0)=−1 হয় তবে f'(2) -এর মান হবে -
06:26View SolutionLet f(x)=(1−x)2sin2x+x2 for all x ∈ R, and let g(x)=∫(2(t−1)t+1−lnt)f(t)dt for t ∈ [1, x] for all x ∈ (1, ∞).Which of the following is true ?
02:45View SolutionLet f(x+y)−f(x)2=f(y)−a2+xy for all real x and y . If f(x) is differentiable and f'(0) exists for all real permissible values of a and is equal to √5a−1−a2 then f(x) is
02:39View SolutionLet f(x+y2)=f(x)+f(y)2∀x,y,∈R.Iff(0)=1.f'(0) exists and equal −1, find f'(2).
View SolutionLet f(x) be a real valued function such that f(0)=12 and f(x+y)=f(x)f(a-y)+f(y)f(a-x),∀x,y∈R, then for some real a,
03:47View Solution

