Question

$f:R\to R$ is defined as $f\left(x\right)=\{\begin{array}{ccc}{x}^2+kx+3\text{,}& & \text{for}x\ge 0\\ 2kx+3\text{,}& & \text{for}x<0\end{array}$. If $f\left(x\right)$ is injective, then find the values of $k$.

Explanation

`f(x) = {{:(x^(2)+kx+3",",,"for "xge0),(2kx+3",",,"for "x lt0):}`
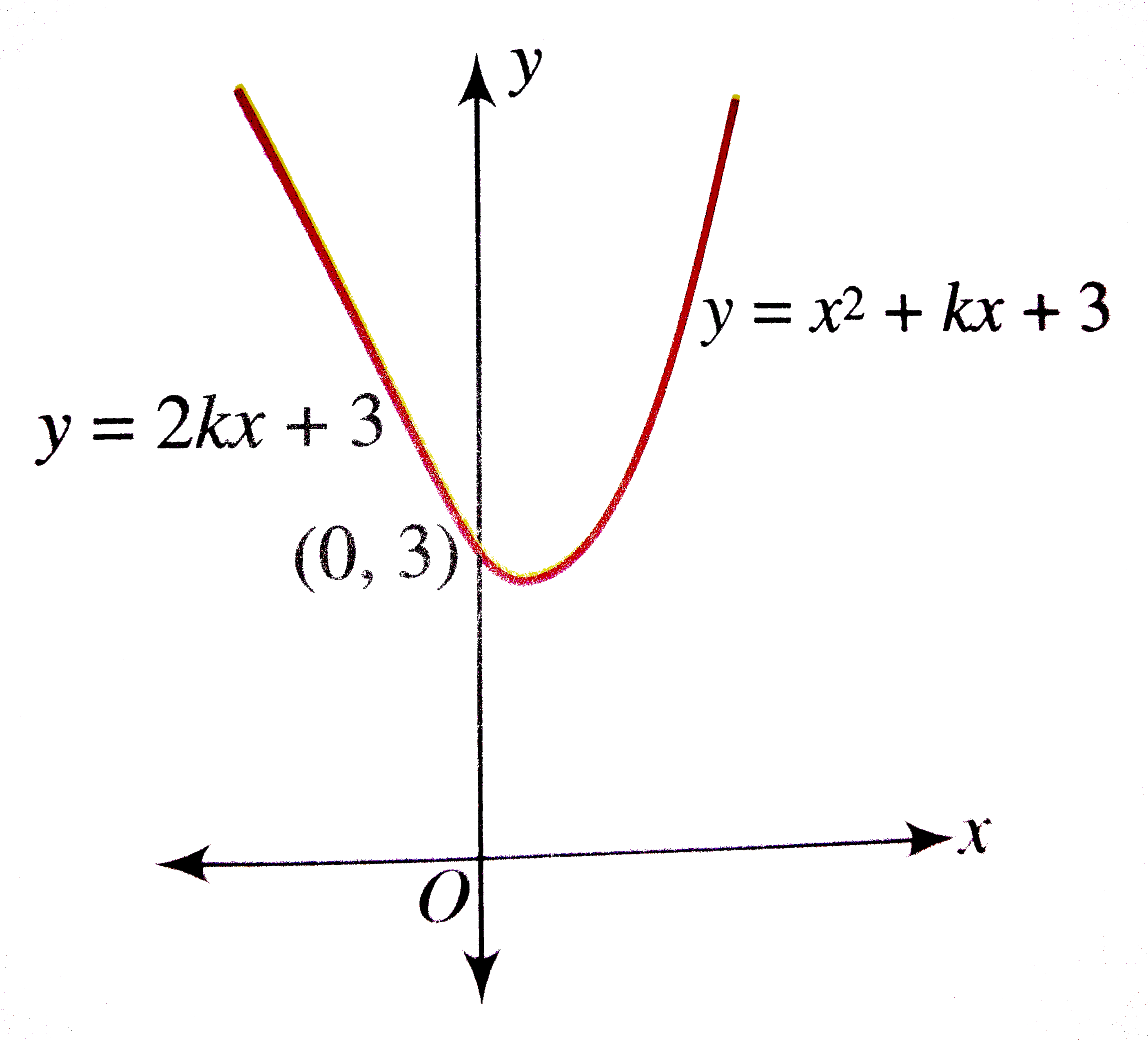
Graph of `y=x^(2)+kx+3` is a variable parabola intersecting the y-axis at (0, 3).
Graph of `y=2kx+3` is a variable straight line passing through (0, 3).
Also the function is continuous, so the possible graph for different values of `k` is as shown in the following figures.
Graph for `k lt 0`

Graph for `k=0`

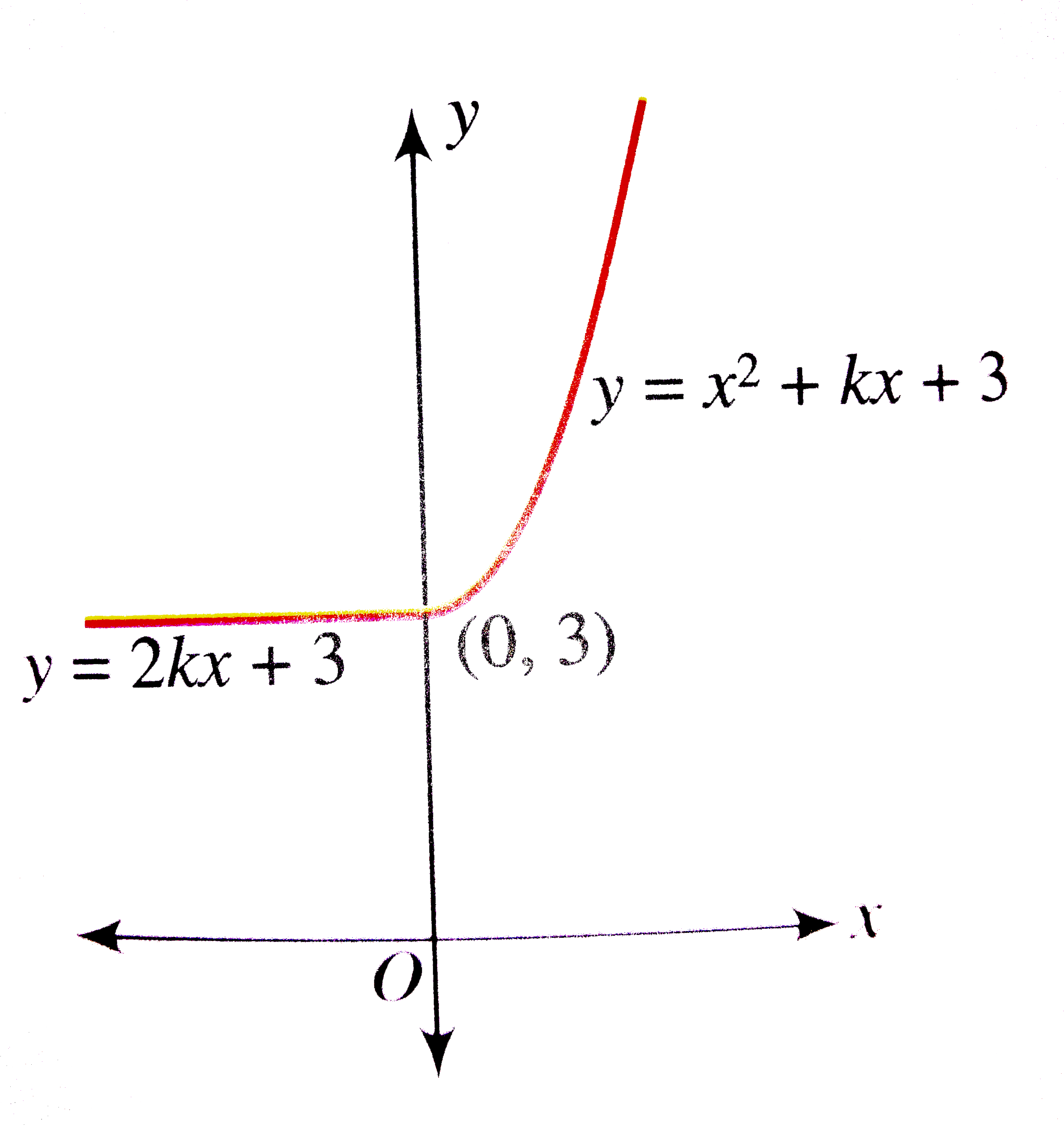
Graph for `k gt 0`

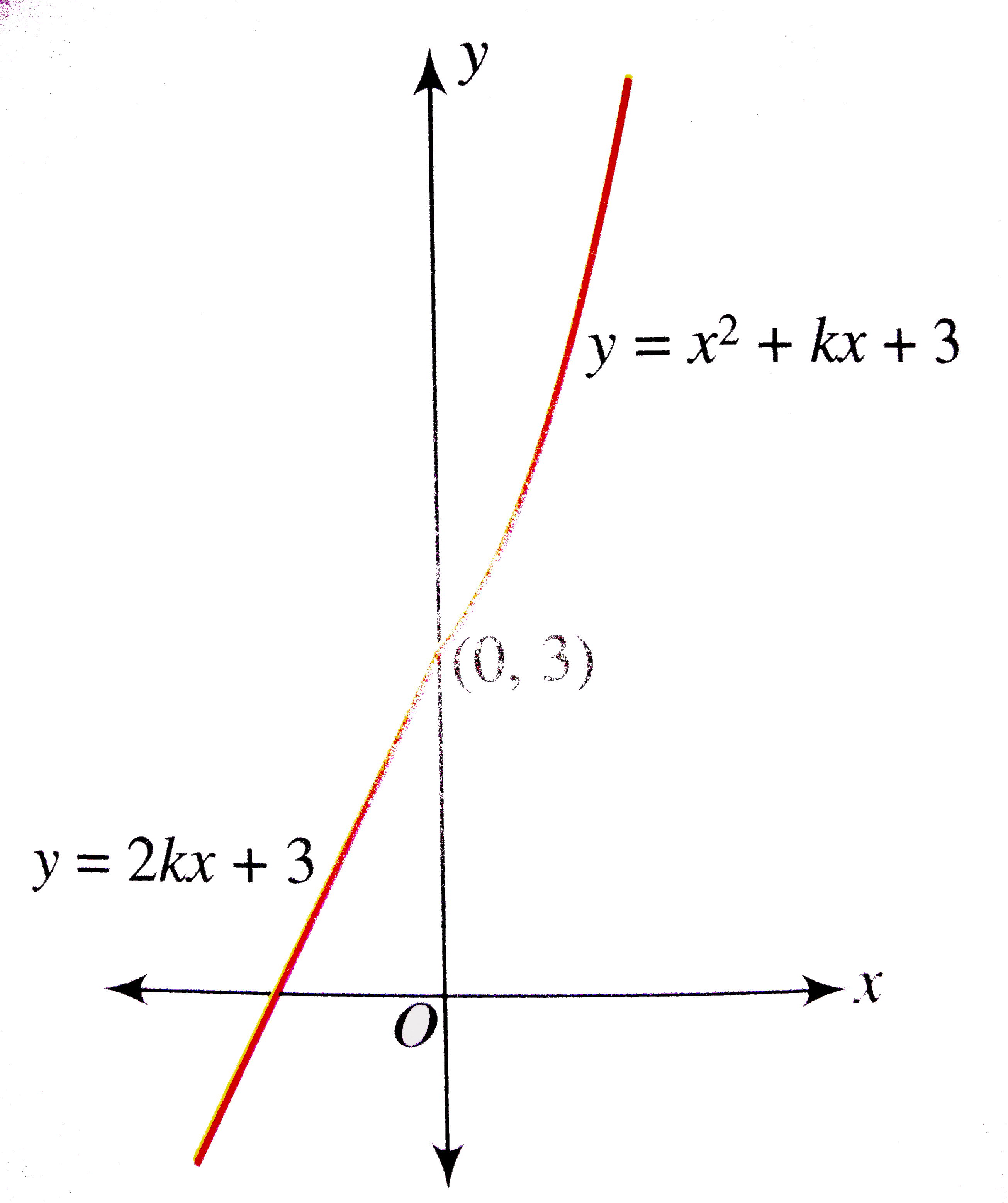
From the above graphs, the possible value of `k` for which the function is injective is `k gt 0`.