The area of the region containing the points (x,y)
satisfying 4≤x2+y2≤2(|x|+|y|)
is
(a)8sq.units
(b) 2sq.units
(c)4πsq.units
(d) 2πsq.unitsSolution in Bengali
The points in the required region satisfy
4≤x2+y2≤2(|x|+|y|) (i)
Since curve (i) is symmetrical about both the axes, the required area is 4 times the area of the region in the first quadrant. Therefore, it is sufficient to sketch the region and to find the area in the first quadrant.
In the first quadrant, curve (i) consists of two curves :
x2+y2≥4 (C1) andx2+y2−2x−2y≥0 (C2)
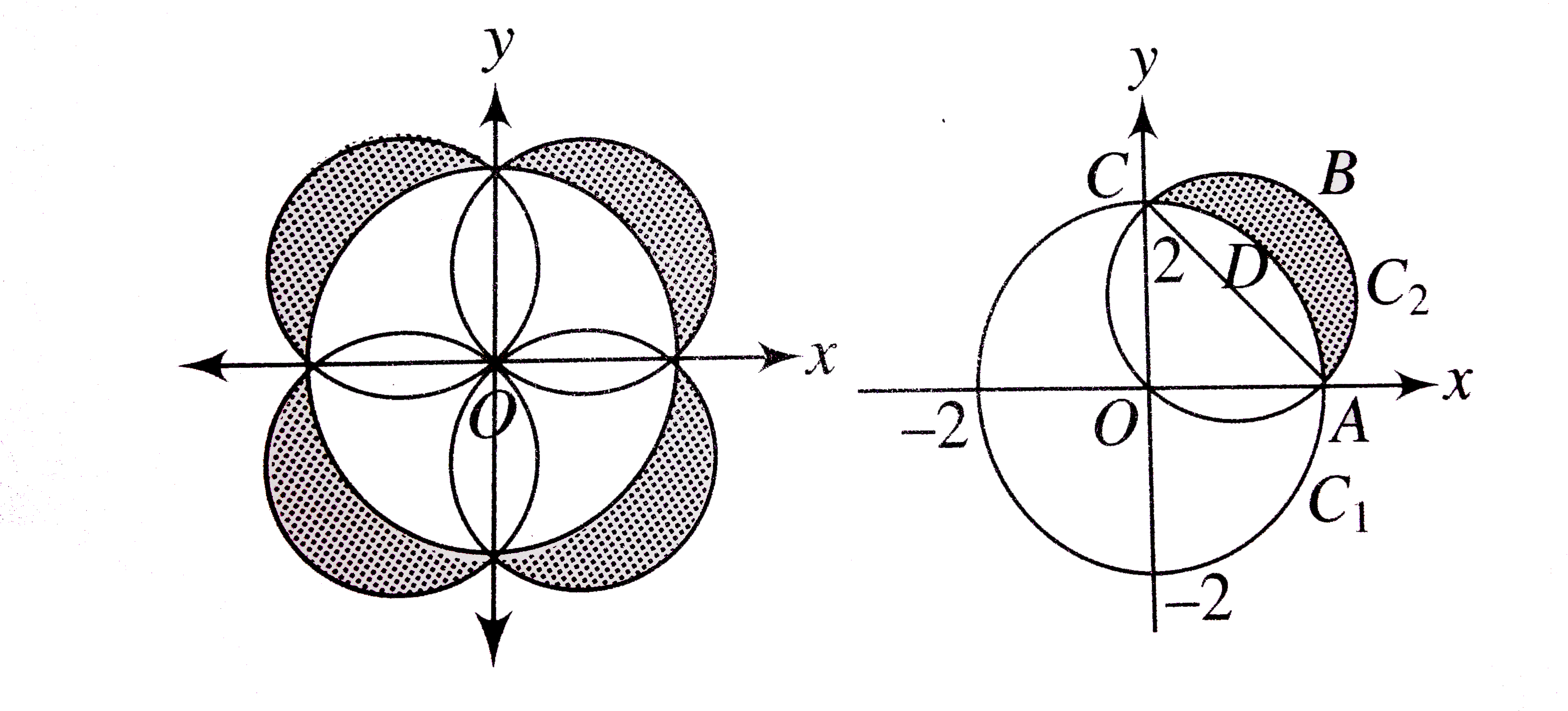
therfore Required area = 4 area ABCDA
= 4 (area of semi-circle ABCA)- (area of sector ADCA)
= 4 (area of semi-circle ABCA)-(area of sector sector OADCO- area of triangle OAC)
=4{π−(π−2)}=8 sq. units
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
11:48View SolutionDraw the graph of y=(x−1)(x2−x+1).
06:31View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
08:39View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
12:16View SolutionIf f(x)=sinx,∀x∈[0,π2],f(x)+f(π−x)=2,∀x∈(π2,π)andf(x)=f(2π−x),∀x∈(π,2π), then the area enclosed by y=f(x) and the x-axis is πsq.units (b) 2πsq.units 2sq.units (d) 4sq.units
07:39View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1andtheabscissaaξsis 163sq.units (b) 103sq.units 133sq.units (d) 73sq.units
06:10View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
04:34View SolutionThe area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|) is (a)8sq.units (b) 2sq.units (c)4πsq.units (d) 2πsq.units
05:08View SolutionA particle of mass m is moving anticlockwise, in a circle of radius R in x−y plane with centre at (R,0) with a constant speed v2. If is located at point (2R,0) at time t=0. A man starts moving with a velocity v1 along the positive y-axis from origin at t=0. Calculate the linear momentum of the particle w.r.t. man as a function of time.
03:35View SolutionThe area of the smaller region bounded by circle x2+y2=1 and |y|=x+1 (a)π2−12sq.units (b) π2−1sq.units (c) π2sq.units (d) π2+1sq.units
04:30View SolutionArea of the triangle formed by the line x+y=3 and angle bisectors of the pair of straight lines x2−y2+2y=1 is 2sq.units b. 4sq.units c. 6sq.units d. 8sq.units
05:57View SolutionThe area of the closed figure bounded by y=x22−2x+2 and the tangents to it at (1,12)and(4,2) is 98sq.units (b) 38sq.units 32sq.units (d) 94sq.units
05:06View SolutionThe area of the loop of the curve ay2=x2(a−x) is 4a2sq.units (b) 8a215sq.units 16a29sq.units (d) None of these
07:49View SolutionThe area bounded by the y=2−x2and x+y=0 is (a)72sq.units b. 92 sq.units c. 9 sq.units d. none of these
06:13View SolutionArea bounded by the curve x y^2=a^2(a-x) and the y-axis is (pia^2)/2s qdotu n i t s (b) pia^2s qdotu n i t s (c) 3pia^2s qdotu n i t s (d) None of these
06:20View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
05:31View Solution

