Iff(x)=min{ 1, x^2 , x^3} then Solution in Bengali
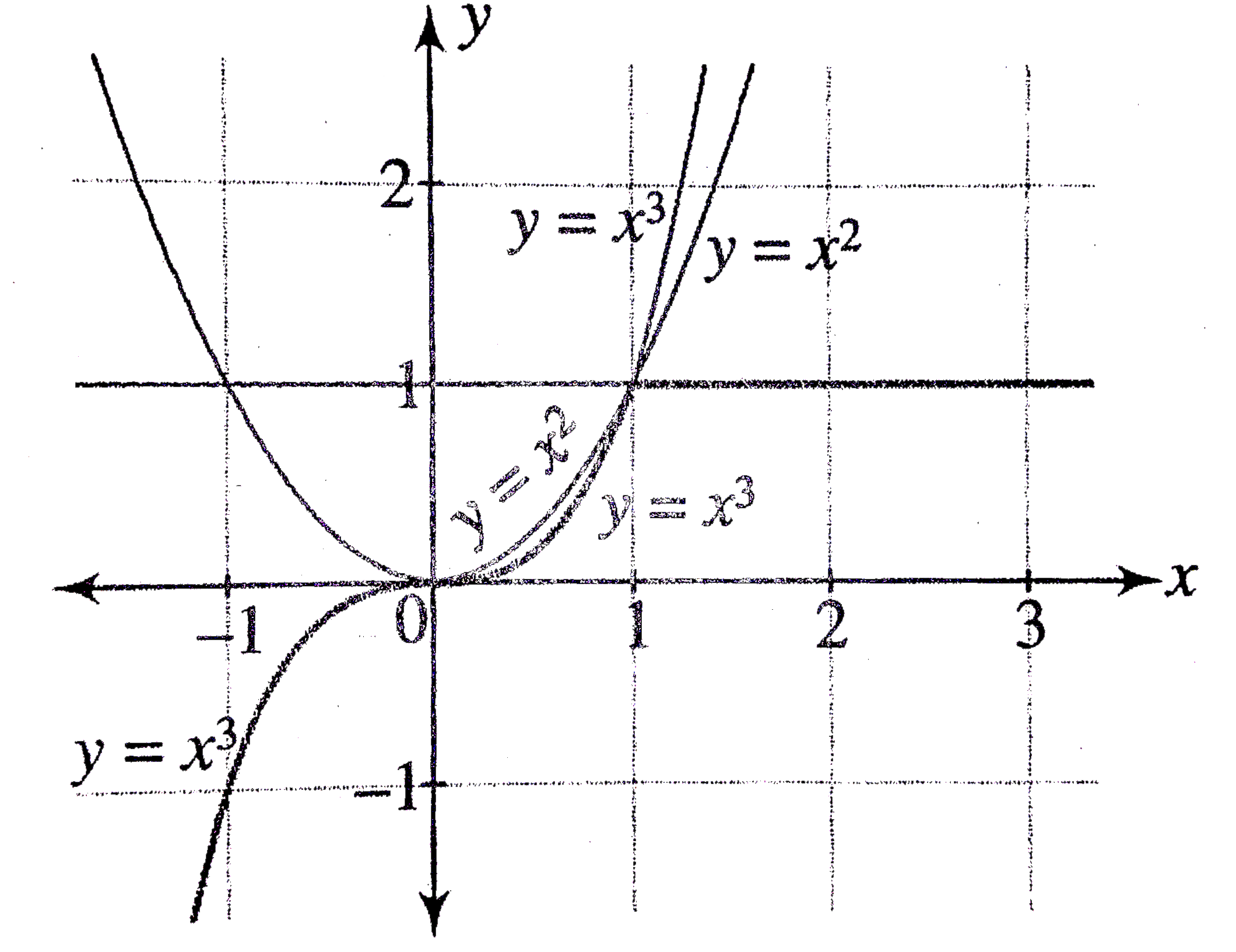
From the graph, y=f(x) is non-differentiable at x=1.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
02:48View SolutionDraw the graph of y=(x−1)(x2−x+1).
06:17View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
03:48View Solutionf(x)=x2+1x2−6x−6x+2 then min value of f(x)
02:27View Solutionf(x)=|x-1|+|x-2|,g(x)=x+(1)/(x),x>0* if m 1=min(f(x)) and m2=min(g(x)) then (m2+m1)/(m2-m1) is equal to
View SolutionIf f(x)=min*(1,x^(2),x^(3)), then
01:30View SolutionCheck the differentiability if f(x)=min.{1,x2,x3}.
03:32View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is01:54View SolutionIf f(x)min(x,x2,x3), then
05:30View Solutionयदि f(x)=min{1,x2,x3}, तब
View SolutionCheck the differentiability if f(x)=min.{1,x2,x3}.
View Solutionf(x)=min{x+2,1,2−x} तब ∫2−2f(x)dx का मान है
01:48View SolutionLet f(x)=f1(x)−2f2(x), where where
f1(x)={min{x2,|x|}|x|≤1min{x2,|x|}|x|>1
and f2(x)={min{x2,|x|}|x|>1min{x2,|x|}|x|≤1and let g(x)={min{f(t):−3t≤x,−3≤x<0}min{f(t):0≤t≤x,0≤x≤3}
For −3≤x≤−1 the range of g(x) is08:35View SolutionLet f(x)=f1(x)−2f2(x), where where
f1(x)={min{x2,|x|}|x|≤1min{x2,|x|}|x|>1
and f2(x)={min{x2,|x|}|x|>1min{x2,|x|}|x|≤1and let g(x)={min{f(t):−3t≤x,−3≤x<0}min{f(t):0≤t≤x,0≤x≤3}
For x∈(−1,0),f(x)+g(x) is03:55View SolutionIff(x)=min{ 1, x^2 , x^3} then
06:10View SolutionThe number of points at which the function,
f(x)={min{|x|,x2}min(2x−1,x2}ifx∈(−∞,1) otherwise is not differentiable is:05:41View Solution

