Question

Two parallel lines lying in the same quadrant make intercepts a and b on x and y axes, respectively, between them. The distance between the lines is
(a) $\frac{ab}{\sqrt{a^2+b^2}}$
(b) $\sqrt{a^2+b^2}$
(c) $\frac{1}{\sqrt{a^2+b^2}}$
(d) $\frac{1}{a^2}+\frac{1}{b^2}$

Options

A. `sqrt(a^(2) + b^(2))`
B. `(ab)/(sqrt(a^(2) + b^(2)))`
C. `(1)/(sqrt(a^(2) + b^(2)))`
D. `(1)/(a^(2))+(1)/(b^(2))`

Answer

B

Explanation

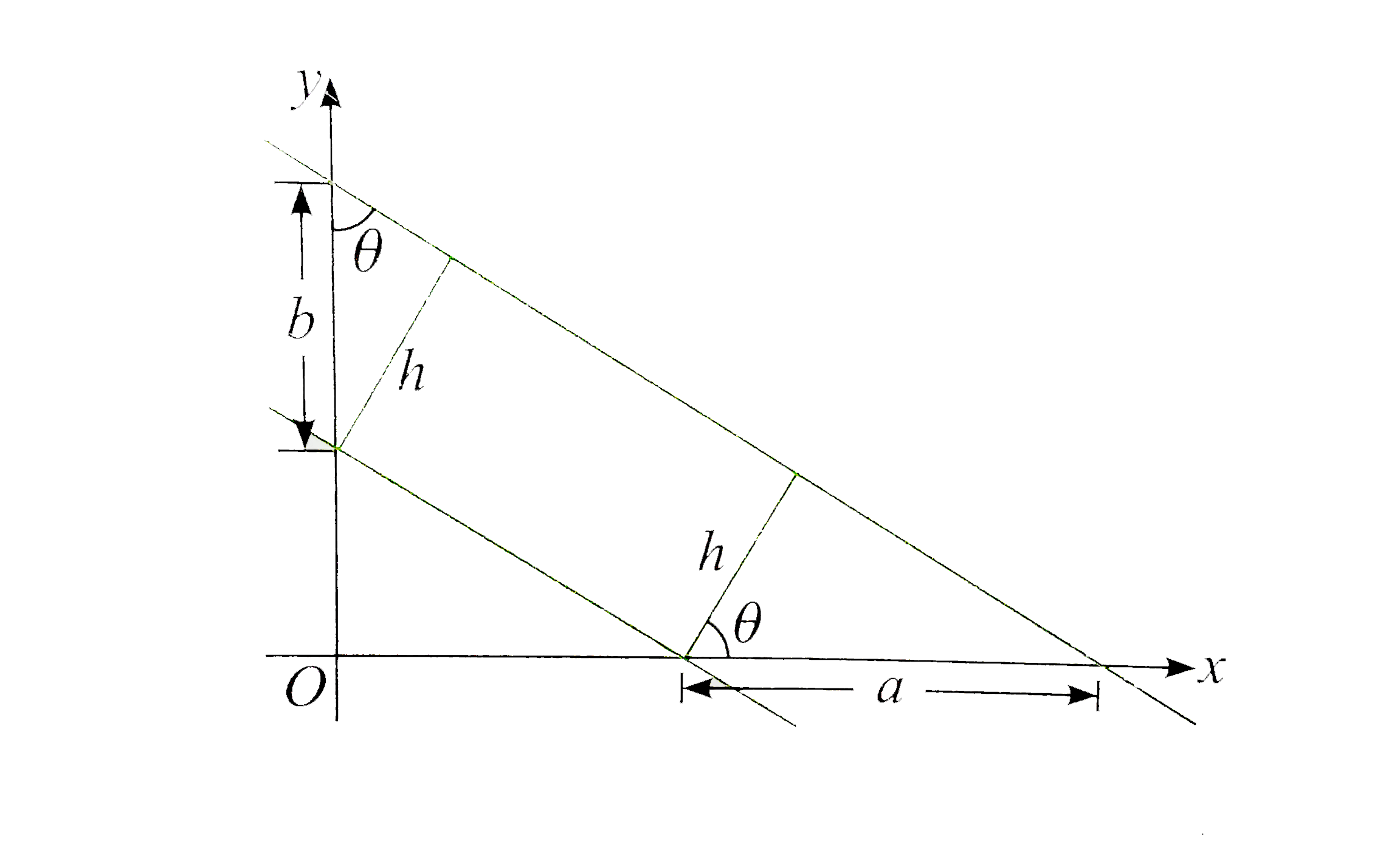
From the figure
`"cos" theta = (h)/(a) " and sin"theta= (h)/(b)`
Squaring these and then adding, we get
`1 = (h^(2))/(a^(2))+ (h^(2))/(b^(2))`
`therefore h = (ab)/(sqrt(a^(2)+ b^(2)))`