A beam of light is sent along the line x−y=1 , which after refracting from the x-axis enters the opposite side by turning through 300 towards the normal at the point of incidence on the x-axis. Then the equation of the refracted ray is (a) (2−√3)x−y=2+√3 (b)(2+√3)x−y=2+√3 (c)(2−√3)x+y=(2+√3) (d)y=(2−√3)(x−1)Solution in Bengali
(2−√3)x−y=2+√3
(2+√3)x−y=2+√3
(2−√3)x+y=(2+√3)
y=(2+√3)(x−1)
The correct Answer is:D
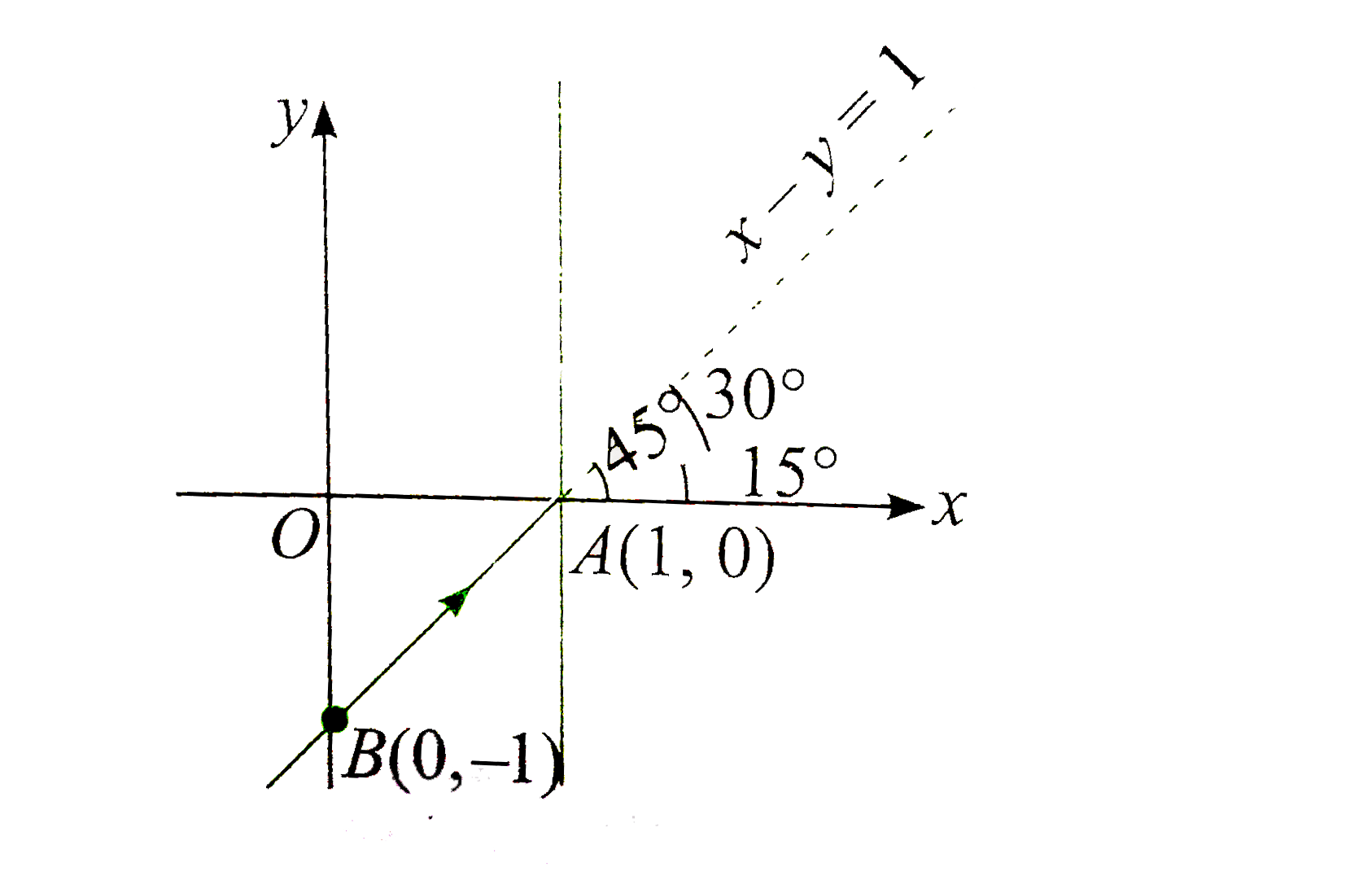
From the figure, the refracted ray makes and angle of 15∘ with the positive direction of the x-axis and passes through the point (1,0). Its equation is
(y−0)=(tan15∘)(x−1)
or y=(2−√3)(x−1)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
04:29View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
03:22View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
02:18View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:14View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
05:22View SolutionA beam of light is sent along the line x−y=1 , which after refracting from the x-axis enters the opposite side by turning through 300 towards the normal at the point of incidence on the x-axis. Then the equation of the refracted ray is (a) (2−√3)x−y=2+√3 (b) (2+√3)x−y=2+√3 (c) (2−√3)x+y=(2+√3) (d) y=(2−√3)(x−1)
07:13View SolutionThe equation of the common tangent touching the circle (x−3)2+y2=9 and the parabola y2=4x above the x-axis is √3y=3x+1 (b) √3y=−(x+3) (C)√3y=x+3 (d) √3y=−(3x−1)
19:32View SolutionThe equation of tangent to the curve y=∫x3x2dt√1+t2 at x=1 is √3x+1=y (b) √2y+1=x √3x+y=1 (d) √2y=x
05:14View Solutionif x=sqrt(3)+(1)/(sqrt(3)) and y=sqrt(3)-(1)/(sqrt(3)) then x^(2)-y^(2) is
02:58View SolutionFind common tangent of the two curve y2=4x and x2+y2−6x=0 (a) y=x3+3 (b) y=(x√3−√3) (c) y=x3−3 (d) y=(x√3+√3)
06:31View SolutionA vertex of an equilateral triangle is at (2, 3), and th equation of the opposite side is x+y=2, then the equaiton of the other two sides are (A) y=(2+√3)(x−2),y−3=2√3(x−2) (B) y−3=(2+√3(x−2),y−3=(2−√3(x−2) (C) y+3=(2−√3(x−2),y−3=(2−√3(x+2) (D) none of these
05:38View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Equation of the sides QR,RP are : (A) y=2√3x+1,y=2√3x−1 (B) y=1√3x,y=0 (C) y=√32x+1,y=√32x−1 (D) y=√3x,y=0
04:38View Solutionयदि x=√3+1√3−1 & y=√3−1√3+1, है तो x2+y2 का मान क्या होगा?
03:25View SolutionIf x=(sqrt(3)+1)/(sqrt(3)-1) and y=(sqrt(3)-1)/(sqrt(3)+1) then find the value of x^(2)+y^(2)
05:16View Solutionx=√3+1√3−1 এবং y=√3−1√3+1 হয়, তবে দেখাও যে, x2+y2x2−y2=7√312
05:10View Solutionx=√3+1√3−1 এবং y=√3−1√3+1 হয়, x2−xy+y2x2+xy+y2-এর সরলতম মান নির্ণয় করো।
09:28View Solution

