A≡(−4,0),B≡(4,0).MandN are the variable points of the y-axis such that M lies below NandMN=4 . Lines AMandBN intersect at P. The locus of P isSolution in Bengali
2xy−16−x2=0
2xy+16−x2=0
2xy+16+x2=0
2xy−16+x2=0
The correct Answer is:D
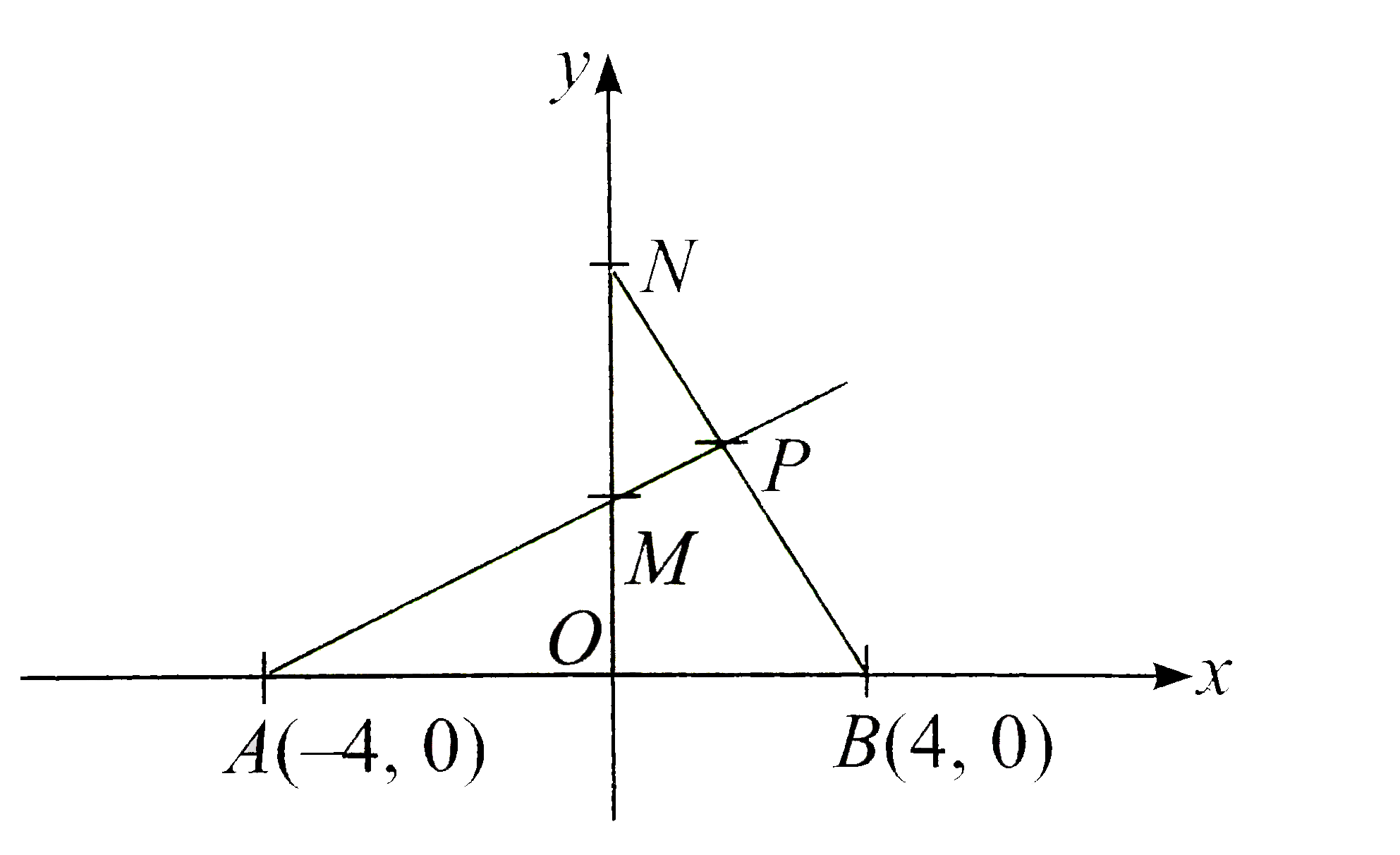
Let M≡(0,h).Then
or N≡(0,h+4)
The equation of AM is
x−4+yh=1
or yh=4+x4
or h=4y4+x
The equation of BN is
x4+yh+4=1
or yh+4=4−x4
or h+4=4y4−x
or h=4y−16+4x4−x
or 4(y−4+x)4−x=4y4+x (Eliminating h)
or 2xy−16+x2=0, which is the required locus
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionAt the point P(a,an) on the graph of y=xn,(n∈N) , in the first quadrant, a normal is drawn. The normal intersects the y−aξs at the point (0,b) . If (lim)a→0=12, then n equals _____.
View SolutionAt the point P(a,an) on the graph of y=xn(n∈N) in the first quadrant at normal is drawn. The normal intersects the Y-axis at the point (0, b). If lima→0b=12, then n equals ……………
View SolutionIf P(A)=0.4,P(B)=p,P(A∪B)=0.6andAandB are given to be independent events, find the value of p.
View SolutionAt the point P(a,an) on the graph of y=xn,(n∈N) , in the first quadrant, a normal is drawn. The normal intersects the y- aξs at the point (0,b) . If (lim)a→0=12, then n equals _____.
View SolutionA≡(−4,0),B≡(4,0).MandN are the variable points of the y-axis such that M lies below NandMN=4 . Lines AMandBN intersect at P. The locus of P is (a) 2xy−16−x2=0 (b) 2xy+16−x2=0 (c) 2xy+16+x2=0 (d) 2xy−16+x2=0
View SolutionA≡(−4,0),B≡(4,0).MandN are the variable points of the y-axis such that M lies below NandMN=4 . Lines AMandBN intersect at P. The locus of P is (a) 2xy−16−x2=0 (b) 2xy+16−x2=0 (c) 2xy+16+x2=0 (d) 2xy−16+x2=0
View SolutionLet MandN be two 3×3 non singular skew-symmetric matrices such that MN=NM. If PT denote the transpose of P, then M2N2(MTN−1)T is equal to M2 b. −N2 c. −M2 d. MN
View SolutionA normal to the hyperbola x2a2−y2b2=1 meets the axes at MandN and lines MP and NP are drawn perpendicular to the axes meeting at P. Prove that the locus of P is the hyperbola a2x2−b2y2=(a2+b2).
View SolutionAt the point P(a,an) on the graph of y=xn(n∈N) in the first quadrant at normal is drawn. The normal intersects the Y-axis at the point (0, b). If lima→0b=12, then n equals ……………
View Solutionआरेख y=xn(n∈N) के बिंदु P(a,an) पर प्रथम चतुर्थांश में एक अभिलम्ब खींचा जाता है। अभिलम्ब y- अक्ष को बिंदु (0,b) पर प्रतिच्छेद करता है। यदि lima→0b=12 हो तब n बराबर है
View Solution
