The number of triangles that the four lines y=x+3,y=2x+3,y=3x+2, and y+x=3 form is (a) 4 (b) 2 (c) 3 (d) 1Solution in Bengali
4
2
3
1
The correct Answer is:C
The lines y=x+3, y=2x+3 and y+x=3 are concurrent at (0,3).
Rough sketch of the lines is as shown in the figure.
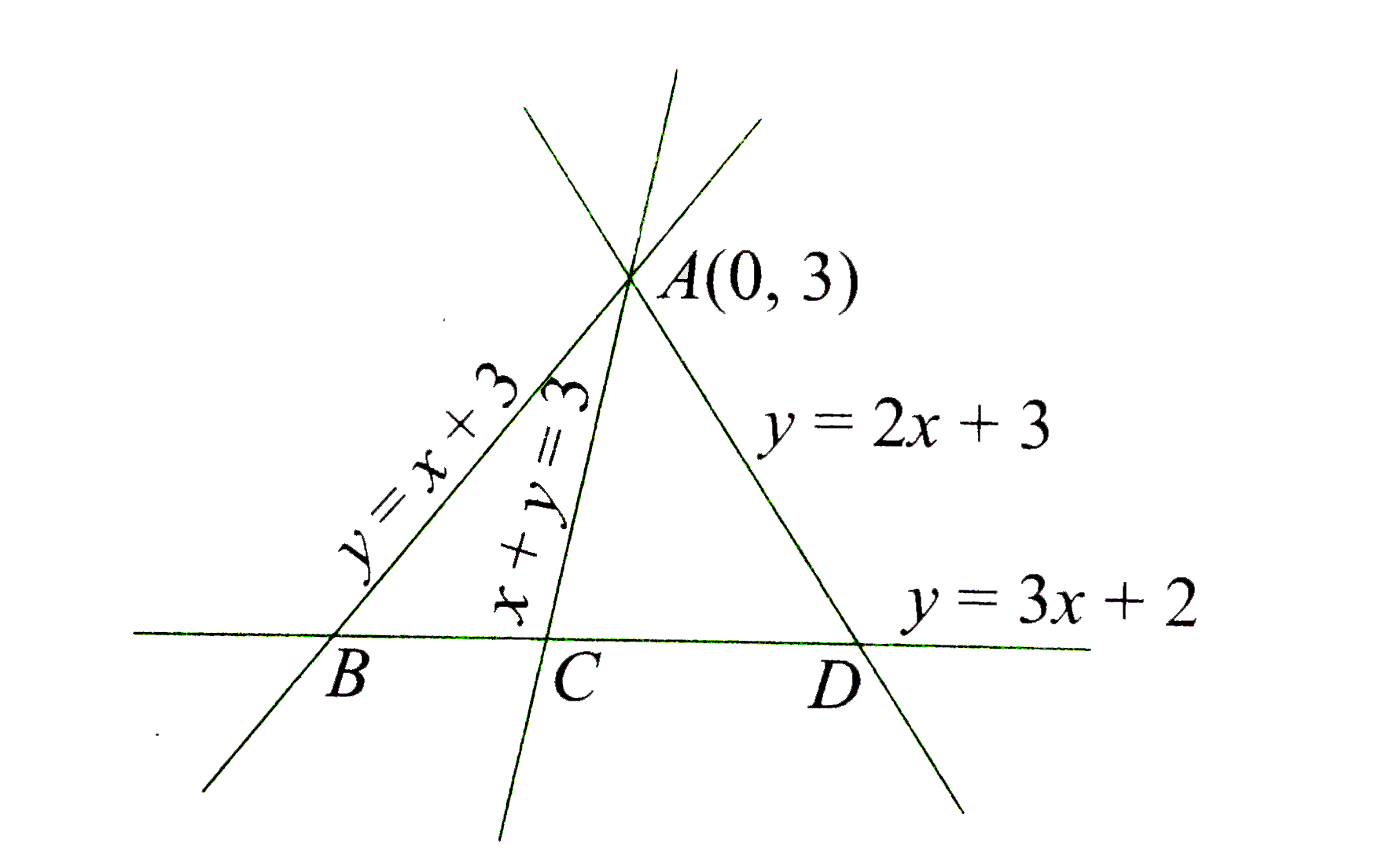
From the figure, three triangles ABD, ABC nad ACD can be formed.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
12:26View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
03:02View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
04:40View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:19View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
06:02View SolutionIf y3−y=2x,then(x2−127)d2ydx2+xdyd= y b. y3 c. y9 d. y27
11:40View SolutionThe number of triangles that the four lines y = x + 3, y = 2x + 3, y = 3x + 2, and y + x = 3 form is (a) 4 (b) 2 (c) 3 (d) 1
08:13View SolutionIf [2x+y4x5x−74x]=[77y−13yx+6] , then the value of x+y is x=3 , y=1 (b) x=2 , y=3 (c) x=2 , y=4 (d) x=3 , y=3
02:43View SolutionWhich of the following line is passing through point of intersection of line x−42=y−32=z−51 and the plane x+y+z=2 (a) x2=y+13=z−34 (b) x−23=y−13=z−32 (c) x2=y+13=z−24 (d) x−22=y+13=z+34
03:31View SolutionThe locus of the centre of the circle passing through (1,1) and cutting x2+y2=4 orthogonally is : (A) x+y=3 (B) x+2y=3 (C) 2x+y=3 (D) 2x−y=3
02:46View Solution(a) Draw the graph for line y=3x.
(b) y=-x
(c) y=2x +4
(d) y=-x+2
(e) y=2x-403:50View SolutionThe number of triangles that the four lines y=x+3,y=2x+3,y=3x+2, and y+x=3 form is (a) 4 (b) 2 (c) 3 (d) 1
04:28View SolutionThe solution of x2+y2dydx=4 is
a. x2+y2=12x+C b. x2+y2=3x+C c. x3+y3=3x+C d. x3+y3=12x+C06:48View SolutionWhich of the following line is passing through point of intersection of line x−42=y−32=z−51 and the plane x+y+z=2 (a) x2=y+13=z−34 (b) x−23=y−13=z−32 (c) x2=y+13=z−24 (d) x−22=y+13=z+34
03:03View SolutionTwo numbers x and y such that x + y=2 and x3y is maximum, are...... A) 1/3, 5/3 B) 3/2, 1/2 C) 1, 1 D) 6/5, 4/5
06:33View Solutionx3−3x2y+y2x−y3 में से 2x3−y3 को घटाइए
06:29View Solution

