Two vertices of a triangle are (4,−3)&(−2,5). If the orthocentre of the triangle is at (1,2), find coordinates of the third vertex .Solution in Bengali
(−33,−26)
(33,26)
(26,33)
none of these
The correct Answer is:B
Let the third vertex be (h,k)
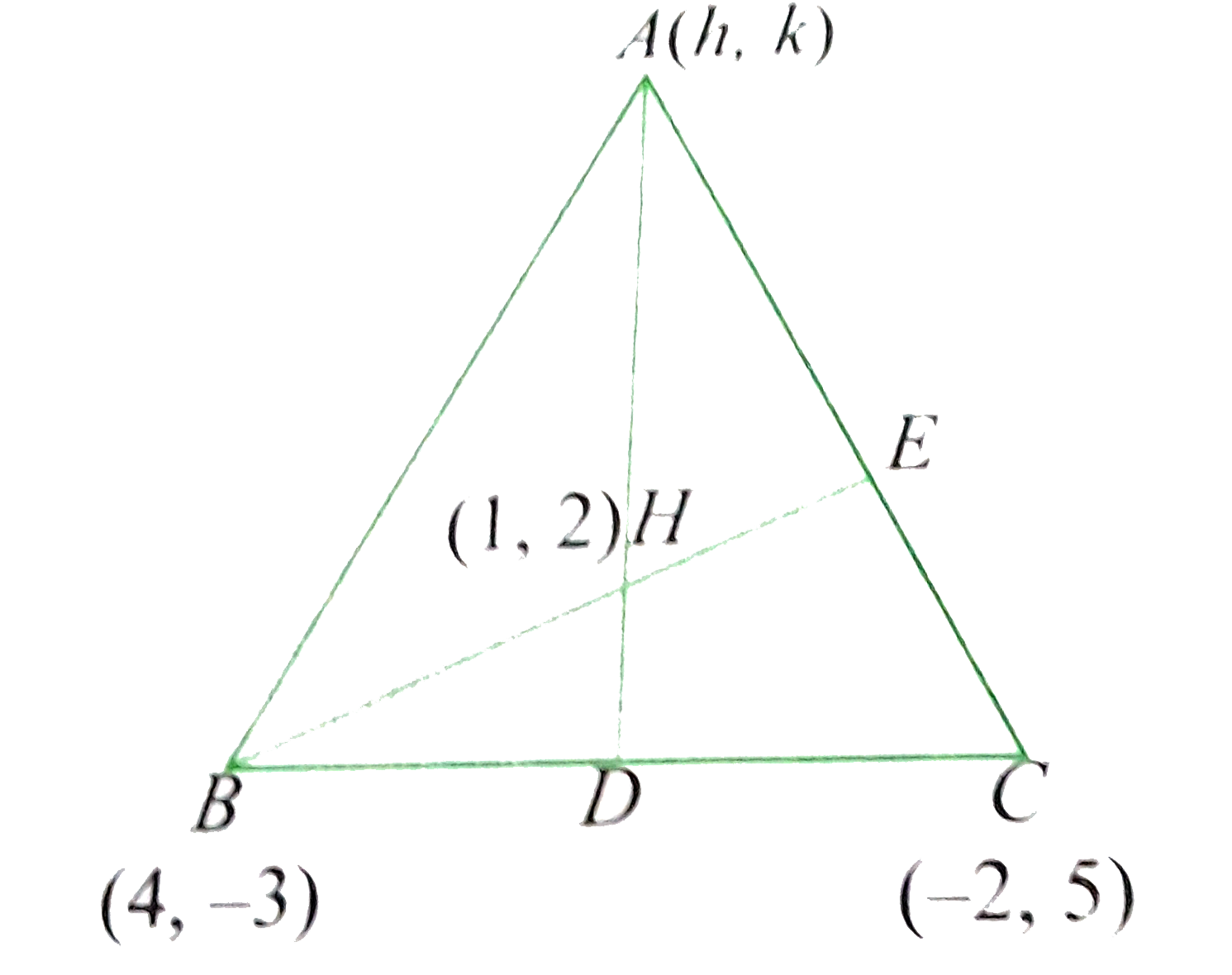
Now, the slope of AD is (k−2)(h−1), the slope of BC is (5+3)/(−2−4)=4/3, the slope of the BE is (−3−2)/(4−1)=−5/3, and the slope of AC is (k−5)(h+2). Since AD⊥BC , we have
k−2h−1×−43=1
or 3h−4k+5=0 (1)
Again, since BE⊥AC, we have
53×k−5h+2=−1
or 3h−5k+31=0
On solving (1) and (2) , we get h=33,h=26, hence, the third vertex is (33,26).
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionFor points P=(x1,y1)and Q=(x2,y2) of the co-ordinate plane a new distance d(P,Q)=|x1−x2|+|y1−y2| is defined .Let O(0,0)and A(3,2). The set of points in first quadrant which are equidistant from O and A is
View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionTwo vertices of a triangle are (3,−1) and (−2,3) and its orthocenter is at the origin,. Find the coordinates of its third vertex.
View SolutionTwo vertices of a triangle are (4,-3)&(-2,5). If the orthocentre of the triangle is at (1,2), find coordinates of the third vertex.
View Solutionएक त्रिभुज के दो शीर्ष (3, -5) और (-7, 4) हैं । यदि त्रिभुज के केन्द्रक के निर्देशांक (2, -1) हों, तो तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए ।
View Solutionयदि एक त्रिभुज के दो शीर्षों के निर्देशांक (1, 2), (3, 5) हैं तथा केन्द्रक मूल बिन्दु है, तो तीसरे शीर्ष के निर्देशांक ज्ञात कीजिये ।
View SolutionThe coordinates of two vertices of a triangle are (-2,3) and (5,-1) . If the orthocentre of the triangle is at the origin , find the coordinates of its third vertex.
View SolutionTwo vertices of triangle are (4 , 3 , -6) , (3 , -4 , 4) and the coordinates of its centroid are ( 2 , - 2 , 1) , find the coordinates of the third vertex of the triangle.
View Solutionकिसी त्रिभुज के दो शीर्षों के निर्देशांक (5, 4) तथा (−2,4) है । यदि त्रिभुज के केन्द्रक के निर्देशांक (5, 6) हों तो तीसरे शीर्ष के निर्देशांक होंगे :
View SolutionTwo vertices of a triangle are (5,-1) and (-2,3). If the orthocentre of the triangle is the origin, find the third vertex.
View Solutionकिसी त्रिभुज के दो शीर्षों के निर्देशांक (1,2) तथा (3,5) है। यदि त्रिभुज का केन्द्रक मूल बिंदु पर है, तो तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए।
View SolutionTwo vertices of a triangle are (4,−3)&(−2,5). If the orthocentre of the triangle is at (1,2), find coordinates of the third vertex .
View Solution