Let ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-Solution in Bengali
1/8
1/4
5/8
3/8
The correct Answer is:C
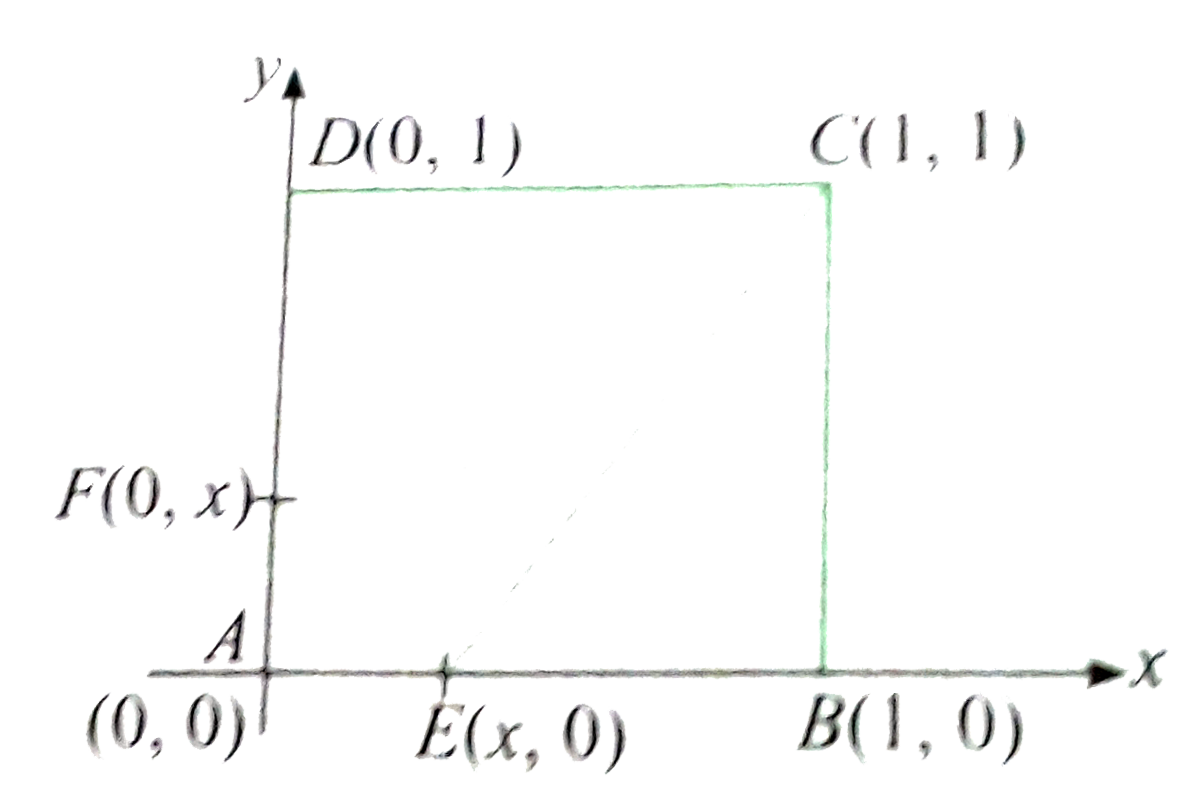
Area of CHEF
A=1−12x2−12(1−x)
=2−2x2−1+x2=1+x−x22=54−(x−12)22
Amax=58atx=12
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type4videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value12videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:
 05:46View Solution
05:46View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
04:09View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
05:43View SolutionLet ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE=AF .Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
06:08View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to06:59View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is01:38View Solutionएक वर्ग ABCD की भुजा AB का मध्य बिंदु F है तथा बिंदु E भुजा BC पर इस प्रकार है की BE=13BC है|यदि ΔFBE का क्षेत्रफल 108 वर्ग सेमि. हो तो विकर्ण AC की लम्बाई ज्ञात करो |
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The maximum area of quandrilateral CDFE will be -03:10View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to -04:37View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. Let a line passing throught point A divides the square ABCD into two parts so that area of one part is double to another , then lenght of the line segment inside the square is -
06:35View SolutionLet ABCD be a quadrilateral with area 18, with side AB parallel to the side CD and AB = 2 CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is :
View SolutionABCD একটি 1 একক বাহুবিশিষ্ট বর্গক্ষেত্র। AB এবং AD- এর ওপর E এবং F বিন্দু দুটি এমনভাবে নেওয়া হল যেখানে AE=AF হয়। মনে করো ABCD বর্গক্ষেত্রের ভিতরে P একটি বিন্দু। CDFE- এর বৃহত্তম সম্ভাব্য ক্ষেত্রফল হবে-
05:00View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to07:51View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is05:44View Solution

