Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is Solution in Bengali
√10/3
√13/3
√11/3
2/√3
The correct Answer is:B
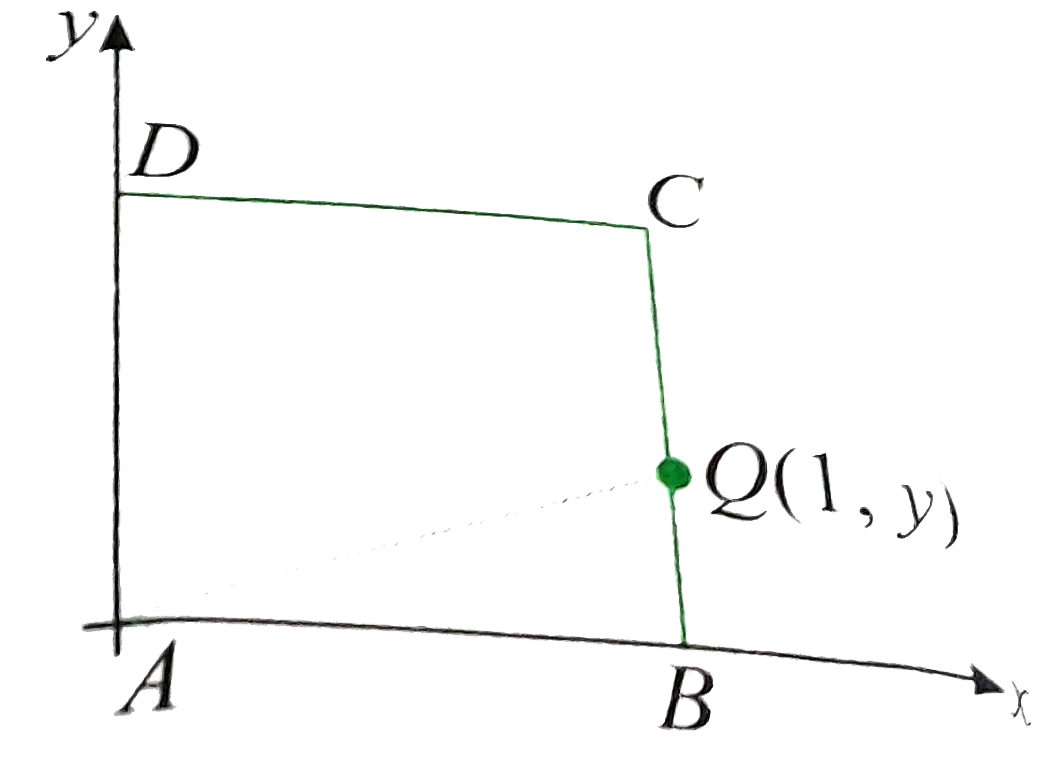
12y(1)=13(1)
or y=23
∴AQ=√(1)2+(23)2=√133
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type4videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value12videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:
 05:46View Solution
05:46View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
04:09View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
05:43View SolutionLet ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE=AF .Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
06:08View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to06:59View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is06:34View Solutionएक वर्ग ABCD की भुजा AB का मध्य बिंदु F है तथा बिंदु E भुजा BC पर इस प्रकार है की BE=13BC है|यदि ΔFBE का क्षेत्रफल 108 वर्ग सेमि. हो तो विकर्ण AC की लम्बाई ज्ञात करो |
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The maximum area of quandrilateral CDFE will be -View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to -03:10View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. Let a line passing throught point A divides the square ABCD into two parts so that area of one part is double to another , then lenght of the line segment inside the square is -
04:37View Solution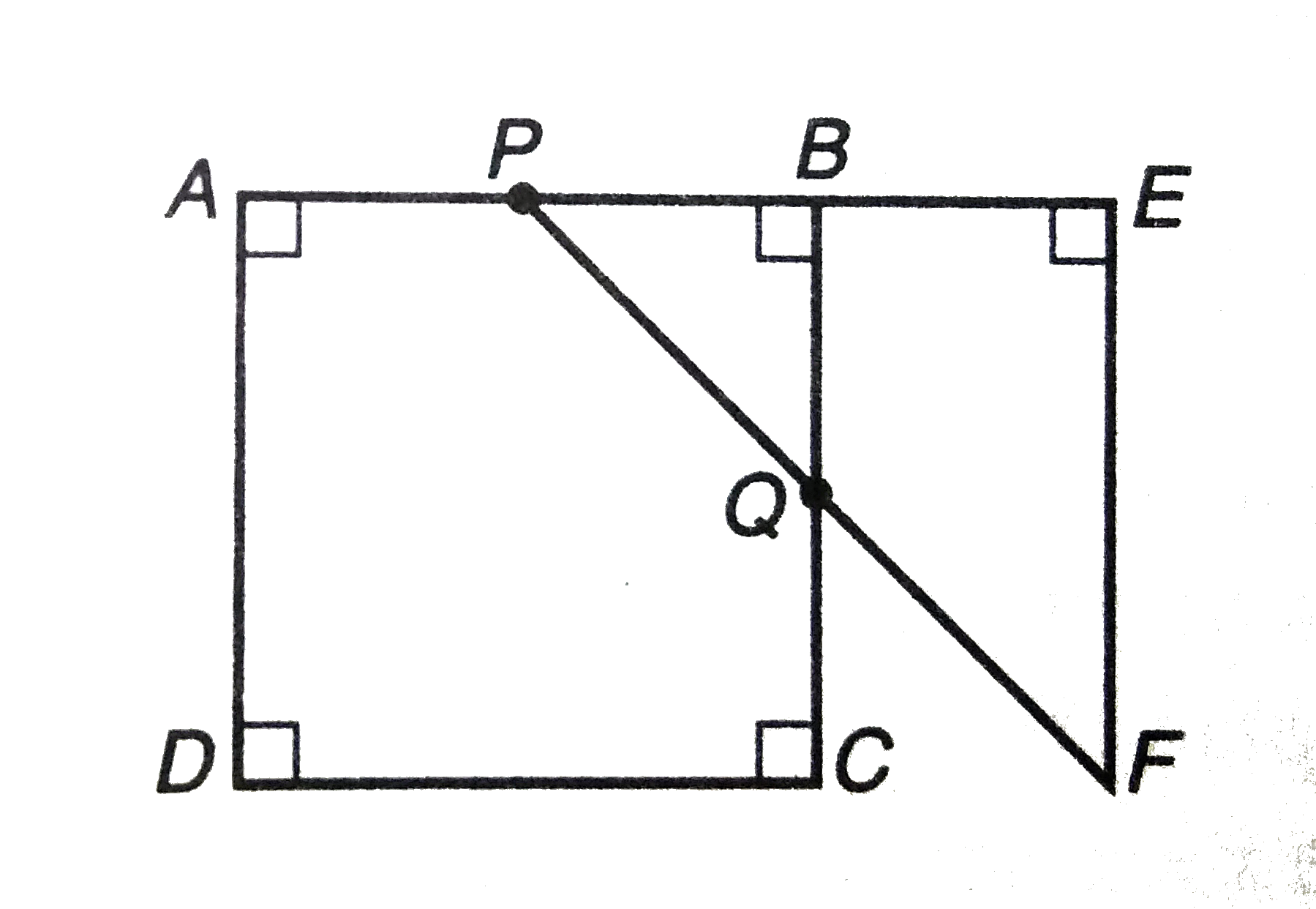
In the figure above, P and Q are the midpoints of sides AB and BC, respectively, of square ABCD. Line segment PB is extended by its own length to point E, and line segment PQ is extended to point F so that FE⊥PE. If the area of square ABCD is 9, what is the area of quadrilateral QBEF?06:35View SolutionABCD একটি 1 একক বাহুবিশিষ্ট বর্গক্ষেত্র। AB এবং AD- এর ওপর E এবং F বিন্দু দুটি এমনভাবে নেওয়া হল যেখানে AE=AF হয়। মনে করো ABCD বর্গক্ষেত্রের ভিতরে P একটি বিন্দু। CDFE- এর বৃহত্তম সম্ভাব্য ক্ষেত্রফল হবে-
View Solutionযদি A বিন্দুগামী কোনো সরলরেখা ABCD বর্গক্ষেত্রকে দুই অংশে এমনভাবে ভাগ করে যে একটি অংশের ক্ষেত্রফল অপর অংশটির দ্বিগুণ হয়, তবে সরলরেখাটির যে পরিমাণ ছেদিতাংশ বর্গক্ষেত্রের ভিতরে থাকবে তার দৈর্ঘ্য হবে-
07:51View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to05:44View Solution

