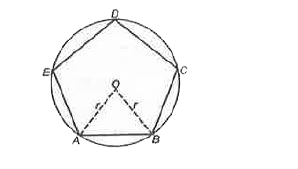
If the area of the circle is $A_{1}$ and the area of the regular pentagon inscribed in the circle is $A_{2},$ then find the ratio $\frac{A_{1}}{A_{2}} .$ Solution in Bengali

Video Solution

Text Solution

Verified by Experts

In $Δ O A B, O A = O B = r$
and $∠ A O B = \frac{360^{\circ}}{5} = 72^{\circ}$
$∴$ Area of $Δ A O B = \frac{1}{2} r \times r {sin 72}^{\circ}$
$= \frac{1}{2} r^{2} {cos 18}^{\circ}$
$∴$ Area of pentagon $(A_{2}) = 5 (Area of Δ A O B)$
$= 5 (\frac{1}{2} r^{2} {cos 18}^{\circ})$ (i)
Also, Area of the circle $(A_{1}) = π r^{2}$ (ii)
Hence, $\frac{A_{1}}{A_{2}} = \frac{π r^{2}}{\frac{5}{2} r^{2} {cos 18}^{\circ}} = \frac{2 π}{5} sec (\frac{π}{10})$
[from Eqs. (i) and (ii)]

Updated on:21/07/2023

|

Class 12 MATHS PROPERTIES AND SOLUTIONS OF TRIANGLE

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-PROPERTIES AND SOLUTIONS OF TRIANGLE-Illustration

Home
Ask Doubt
Profile