The circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.Solution in Bengali
The correct Answer is:36π sq. unit
In the figure, circumcircle of equilateral triangle ABC has circumference 24π.
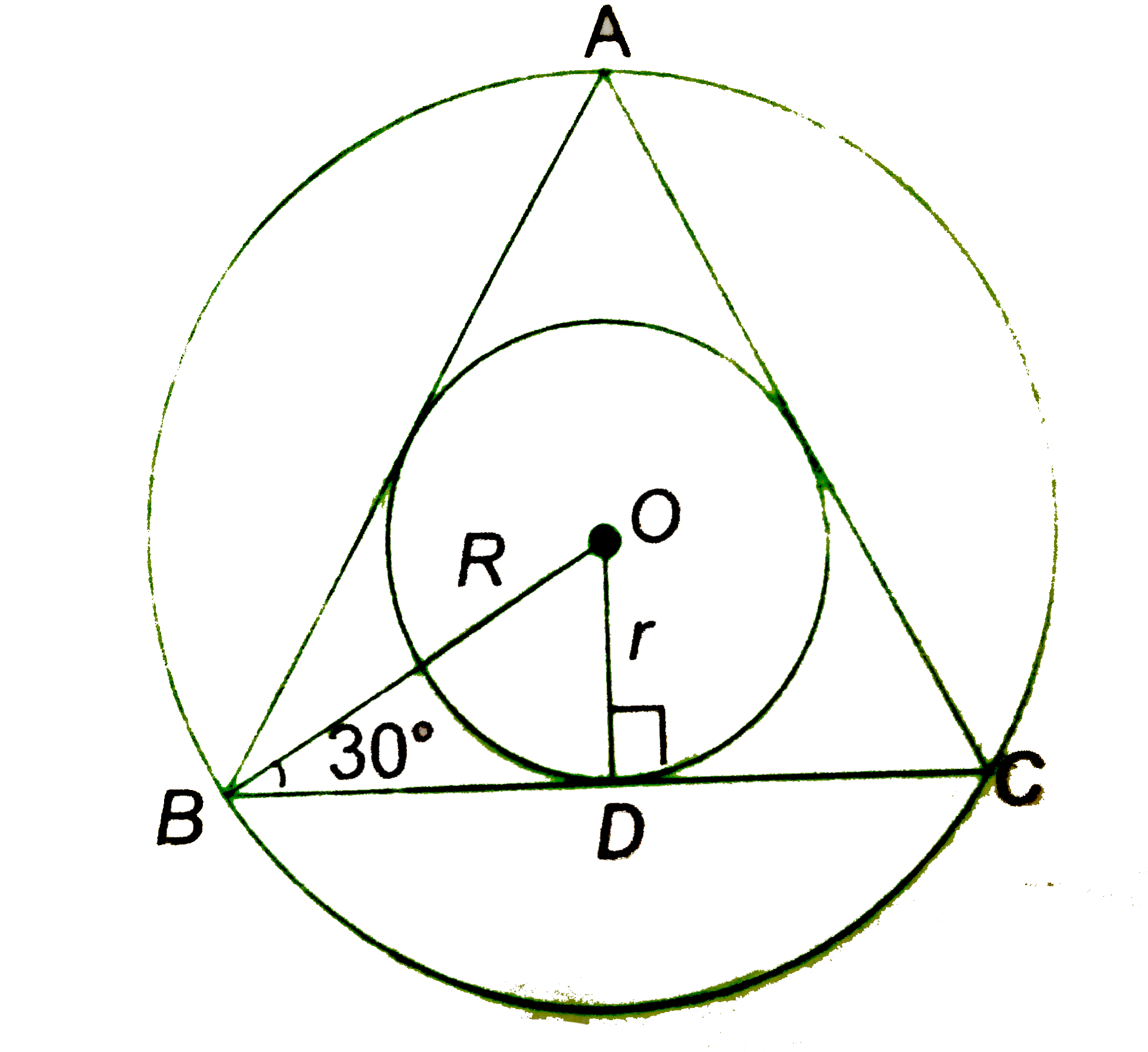
Let R be the radius of the circle and O be the centre.
∴2πR=24π
⇒R=12
Circle inscribed in triangle touches BC at D, which is midpoint of BC.
In triangle ODB, sin30∘=ODOB=rR (r is the radius of incircle)
∴r=122=6
∴ Area of inscrived circle =πr2=36π sq. unit
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.28videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.34videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example10videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)2videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
Prove that sinx−cosx+1sinx+cosx−1=secx+tanx
02:37View SolutionA horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight, and describes 88 metres when it traces 72∘ at the centre, find the length of the rope.
03:54View SolutionIf 2cosx+sinx=1, then find the valie of 7x+6sinx.
01:44View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
05:38View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
03:41View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is
05:27View SolutionThe circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.
07:13View SolutionThe area of an equilateral triangle inscribed in a circle of radius 4cm, is
06:29View SolutionThe area of an equilateral triangle,inscribed in a circle is 16V3cm2. The area of the circle in terms of ? will be- -66.
06:59View SolutionThe area of a circle inscribed in an equilateral triangle is 154cm^(2). Find the perimeter of the triangle.
05:38View SolutionAn equilateral triangle has a circle inscribed in it and is circumscribed by a circle.There is another equilateral triangle inscribed in the inner circle.Find the ratio of the areas of the outer circle and the inner equilateral triangle.
06:46View SolutionAn equilateral triangle has a circle inscribed in it and is circumscribed by a circle. There is another equilateral triangle inscribed in the inner circle. Find the ratio of the areas of the outer circle and the inner equilateral triangle.
05:16View Solution
An equilateral triangle with side 12 is inscribed in a circle . Find the shaded area .03:13View SolutionAn equilateral triangle with a perimeter of 12 is inscribed in a circle. What is the area of circle?
02:31View SolutionA circle is inscribed ina n equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is
08:19View SolutionA circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View Solution

