In an equilateral triangle, three coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. The area of the triangle is 2sqrt(3)(b)6+4sqrt(3)12+(7sqrt(3))/4(d)3+(7sqrt(3))/4Solution in Bengali
The correct Answer is:(4√3+6) sq. unit
The given arrangement of coins is as shown in the given figure.
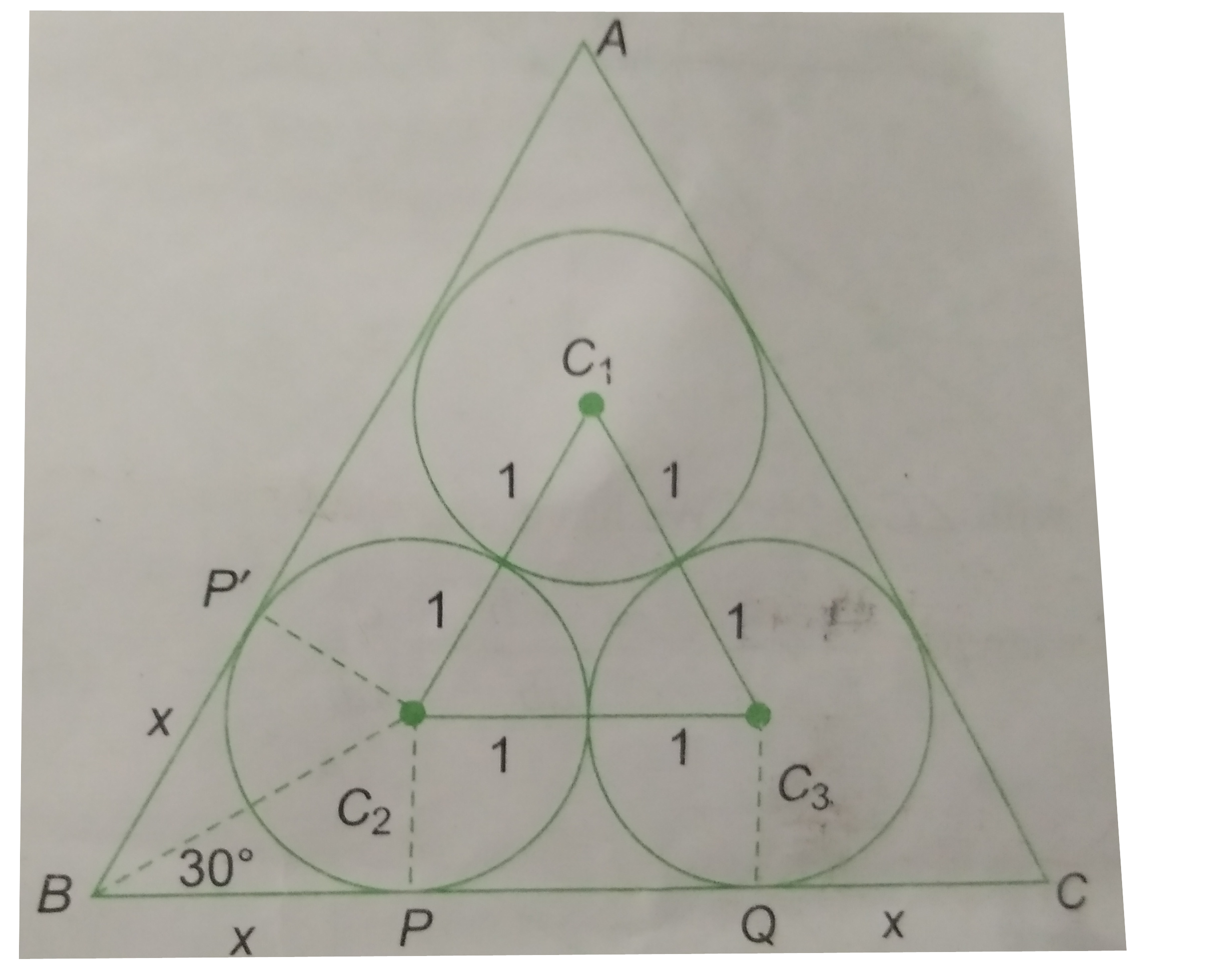
To find the area of the triangle, we need to find its side.
For circle with centre C2, BP and BP' are two tangents from B to circle,
Therefore, BC2 must be angle bisector of ∠B.
∠B=60∘ (∴ΔABC is equilateral)
∴∠C2BP=30∘
∴tan30∘=1x
⇒x=√3
∴BC=BP+PQ+QC
=x+2+x=2+2√3
Area of an equilateral triangle is √34a2, where a is side length.
∴Area of ΔABC=√34(2+2√3)2
=√3(1+3+2√3)
=(4√3+6) sq. unit
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.28videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.34videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example10videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)2videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
Prove that sinx−cosx+1sinx+cosx−1=secx+tanx
02:04View SolutionA horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight, and describes 88 metres when it traces 72∘ at the centre, find the length of the rope.
05:51View SolutionIf 2cosx+sinx=1, then find the valie of 7x+6sinx.
03:09View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
03:09View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
01:30View SolutionIn an equilateral triangle, three coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. The area of the triangle is (fig) 4:2√3 (b) 6+4√3 12+7√34 (d) 3+7√34
02:07View SolutionOne angle of an isosceles triangle is 1200 and the radius of its incircle is √3. Then the area of the triangle in sq. units is
(a) 7+12√3 (b) 12−7√3 (c) 12+7√3 (d) 4π01:04View SolutionIn an equilateral triangle,3 coins of radii 1 unit each are kept so each other and also the side of the triangle.the area of the triangle is:
06:17View SolutionIn an equilateral triangle, three coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. The area of the triangle ABC is
06:44View SolutionThe area of an equilateral triangle is 4√3 cm2. The length of each of its side is (a)3 cm (b) 4 cm (c)2√3 cm (d) √32 cm
02:06View SolutionEach side of an equilateral triangle is equal to the radius of a circle whose area is 154 cm2. The area of the triangle is (a)7√34 cm2 (b) 49√32 cm2 (c)49√34 cm2 (d) 7√32 cm2
03:04View Solution4√3−7√12+2√75=
06:31View SolutionIn an equilateral triangle 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. Are of the triangle is- 4+2√3 b. 6+4√3 c. 12+7√34 d. 3+7√34
02:21View SolutionIn an equilateral triangle, three identical coins of radii 1 units each, are kept so that they touch each other and also the sides of a triangle. Find the area of the triangle.
05:00View SolutionThe area of an equilateral triangle is 4√3cm2. Then the of each of the sides of the triangle is
03:46View SolutionIf the sides of an equilateral triangle be increased by 2 cm each, the area of the triangle is increased by 2√3cm2. Determine the length of each sides of the equilateral triangle.
09:47View Solution

