Let f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2Solution in Bengali
3
0
1
2
The correct Answer is:A
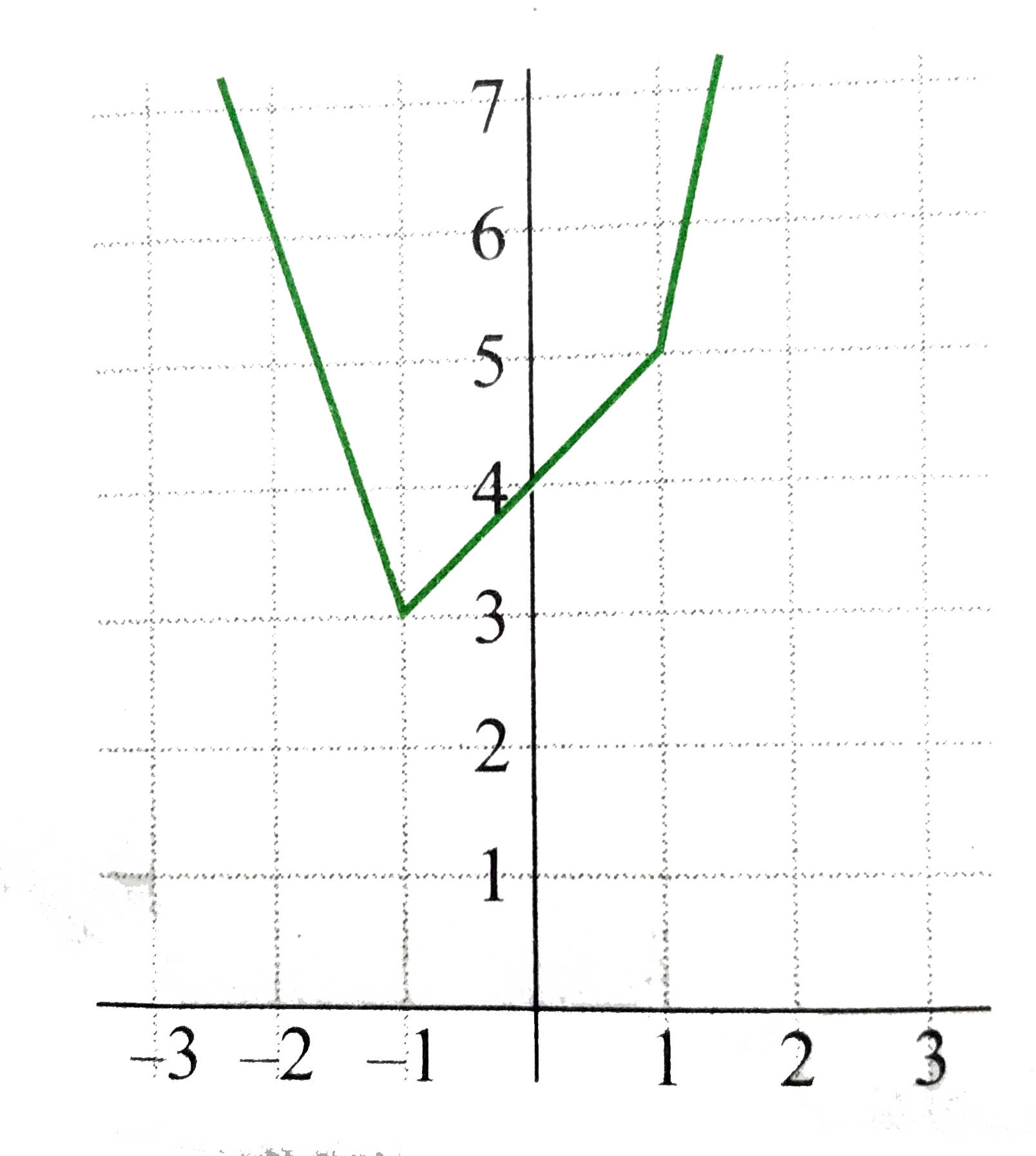
Let f(x)=x+2|x+1|+2|x−1|
=⎧⎪⎨⎪⎩x−2(x+1)−2(x−1),x<−1x+2(x+1)−2(x−1),−1≤x≤1x+2(x+1)+2(x−1),x>1
=⎧⎪⎨⎪⎩−3x,x<−1x+4,−1≤x≤15x,x>1
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
09:11View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 604:47View SolutionLet n_k be the number of real solutions |x+1|+|x-3|=K , then (a) n_K = 0 if K lt 4 (b) n_K = 2 if K gt 4 (c) n_K is infinitely many if K = 4 (d) Minimum value of f(x) = |x+1|+|x-3| is 2
05:18View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
02:09View SolutionIf x is real and k=(x^(2)-x+1)/(x^(2)+x+1) then: (A) (1)/(3)<=k<=3(B)k<=5(C)k<=0(D) none
05:44View SolutionNumber of real values of k for which the equation x+2kx−1=x has exactly one real solution is (A) 0 (B) 1 (C) 2 (D) 3
03:05View SolutionIf |x−1|+|x−2|+|x−3|=k,xεR then value of k for which given equation has exactly one solution.
08:14View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.03:35View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:06:54View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
05:48View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.07:40View SolutionLet f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2
03:41View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:09:44View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:05:22View SolutionLet f(x)=|x−1|+|x−2|+|x−3| , match the column I for the value of k column II.
Column - I Column -II(A) f(x) = k has no solution (p) 1 (B) f(x)=k has only one solution(q) 2 (C) f(x) = k has two solution of same sign (r) 4(D) f(x)= k has two solution of opposite sign(s) 5(t) 804:59View SolutionIf |x−1|+|x−2|+|x−3|=k,xεR then value of k for which given equation has exactly one solution.
05:32View Solution

