Two parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.Solution in Bengali
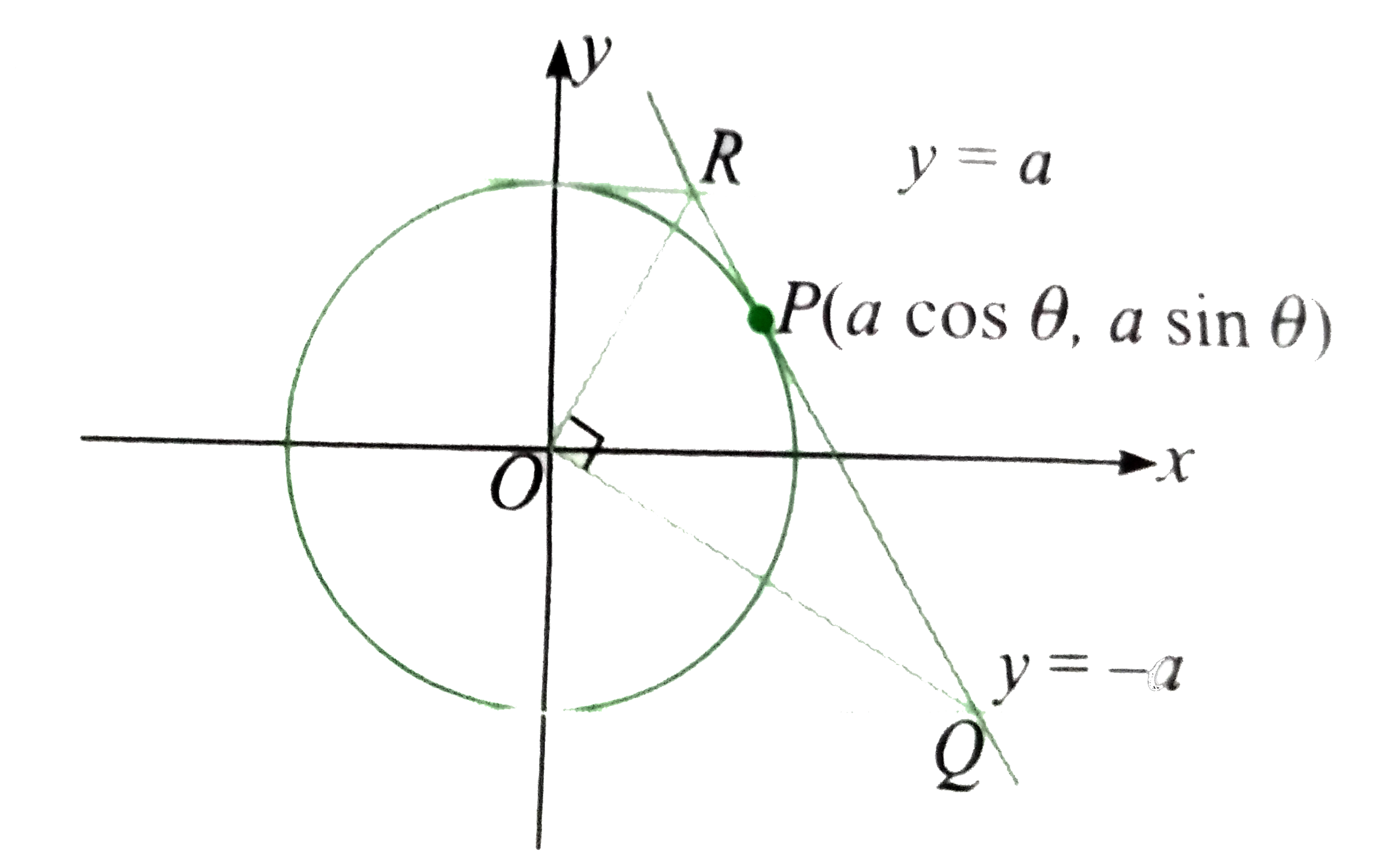
Consider the circle x2+y2=a2.
Let the two parallel tangents be y=a and y=−a.
Third tangent at point P(acosθ,asinθ) is cosθx+sinθy=a.
Solving these with y=±a, we get x=a−+asinθcosθ
∴R≡(a−asinθcosθ,a) and Q≡(a+asinθcosθ,−a)
Slope of OR, m1=aa−asinθcosθ=cosθ1−sinθ
Slope of OQ, m2=−aa+asinθcosθ=−cosθ1+sinθ
m1×m2=cosθ1−sinθ×(−cosθ1+sinθ)=−cos2θ1−sin2θ=−1
Thus, QR subtends right angle at centre.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples13videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
04:54View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
03:20View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:03View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is02:24View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB depends on the radius of the circle. depends on the center of the circle. depends on the slopes of three tangents. is always constant
04:45View Solutionसिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींची गया लम्ब वृत्त के केन्द्र से होकर जाता है।
04:20View Solutionसिद्ध कीजिए कि वृत्त कि दो समान्तर स्पर्शियों के स्पर्श बिन्दु को मिलाने वाली रेखा वृत्त का व्यास होती है।
06:05View Solutionचित्र में,l और m, एक वृत्त पर बिंदुओं A और B पर दो समानान्तर स्पर्श रेखाएँ हैं। यदि वृत्त पर बिंदु पर खींची गई स्पर्श रेखा , स्पर्श रेखाओं l और m के बीच DE अन्तः खण्ड काटती हैं और F वृत्त का केंद्र हैं ,तो सिद्ध करो कि ∠DEF=90∘
03:08View SolutionIn the adoining figure, A is the centre of the circle. Poin D is in the exterior of the circle. Line DP and Line DQ are tangents at points at P and Q respectively. Prove that DP=DQ.
06:47View SolutionPerpendiculars are drawn, respectively, from the points PandQ to the chords of contact of the points QandP with respect to a circle. Prove that the ratio of the lengths of perpendiculars is equal to the ratio of the distances of the points PandQ from the center of the circles.
06:15View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
06:26View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB (a)depends on the radius of the circle. (b)depends on the center of the circle. (c)depends on the slopes of three tangents. (d)is always constant
06:57View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾ 'ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ।
06:41View SolutionIn the picture a triangle is formed by two mutually perpendicular tangents to a circle and a third tangent. Prove that the perimeter of the triangle is equal to the diameter of the circle.
05:09View SolutionThe chord of contact of tangents from a point P to a circle passes through Qdot If l_1a n dl_2 are the length of the tangents from Pa n dQ to the circle, then P Q is equal to
04:36View Solution

