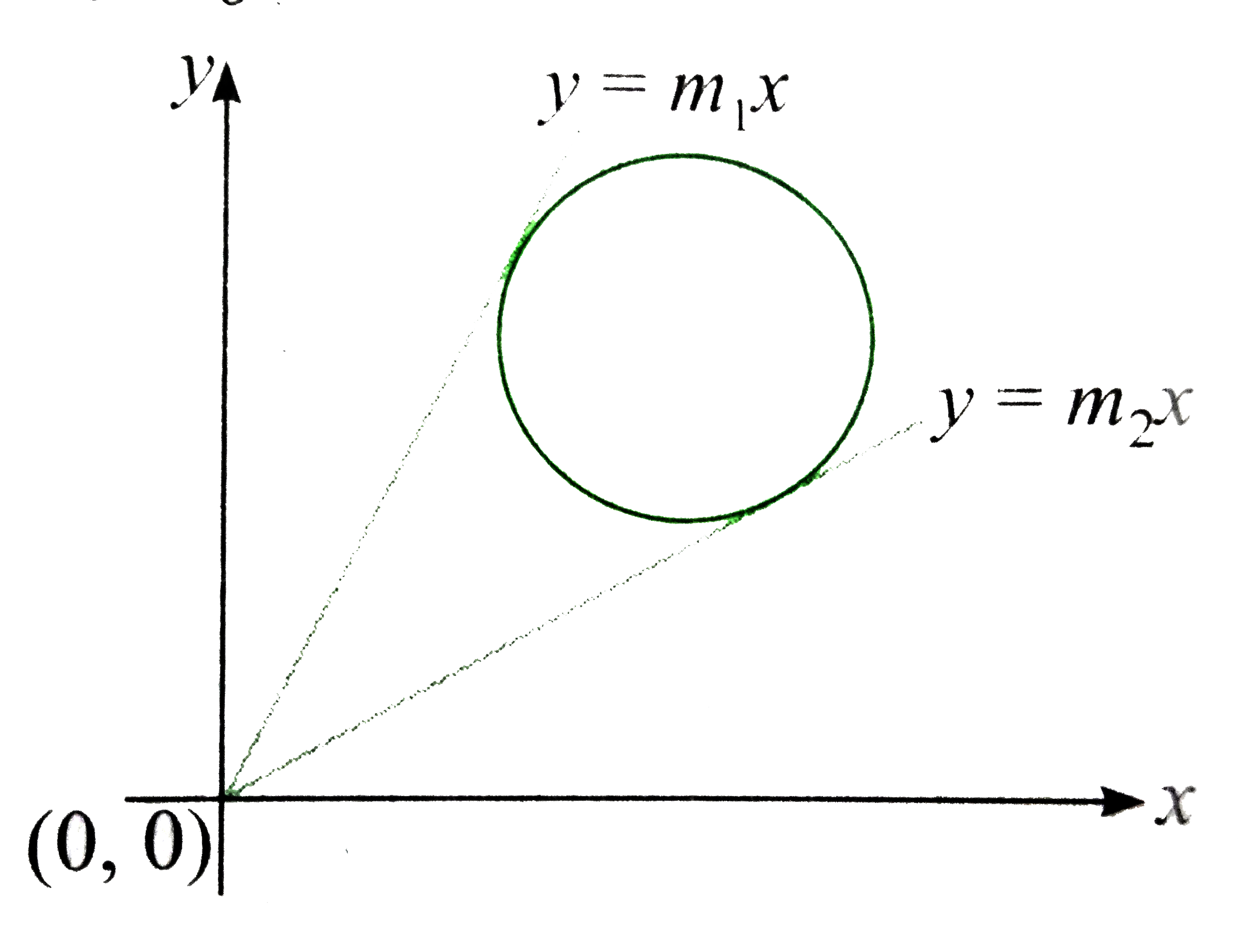
Consider a circle $x^{2} + y^{2} + a x + b y + c = 0$ lying completely in the first quadrant. If $m_{1} a n d m_{2}$ are the maximum and minimum values of $\frac{y}{x}$ for all ordered pairs $(x, y)$ on the circumference of the circle, then the value of $(m_{1} + m_{2})$ is $\frac{a^{2} - 4 c}{b^{2} - 4 c}$ (b) $\frac{2 a b}{b^{2} - 4 c}$ $\frac{2 a b}{4 c - b^{2}}$ (d) $\frac{2 a b}{b^{2} - 4 a c}$ Solution in Bengali

A

$\frac{a^{2} - 4 c}{b^{2} - 4 c}$

B

$\frac{2 a b}{b^{2} - 4 c}$

C

$\frac{2 a b}{4 c - b^{2}}$

D

$\frac{2 a b}{b^{2} - 4 a c}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

Substituting $y = m x$ in the equation of circle, we get
$x^{2} + m^{2} x^{2} + a x + b m x + c = 0$
$(y / x$ denotes the slope of the tangent from the origin on the circles. )
Since the line is touching the circle, we must have discriminant.
${(a + b m)}^{2} - 4 c (1 + m^{2}) = 0$ or $a^{2} + b^{2} m^{2} + 2 a b m - 4 c - 4 c m^{2} = 0$
or $m^{2} (b^{2} - 4 c) + 2 a b m + a^{2} - 4 c = 0$
This equation has two roots $m_{1}$ and $m_{2}$ . Therefore, $m_{1} + m_{2} = - \frac{2 a b}{b^{2} - 4 c} = \frac{2 a b}{4 c - b^{2}}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile