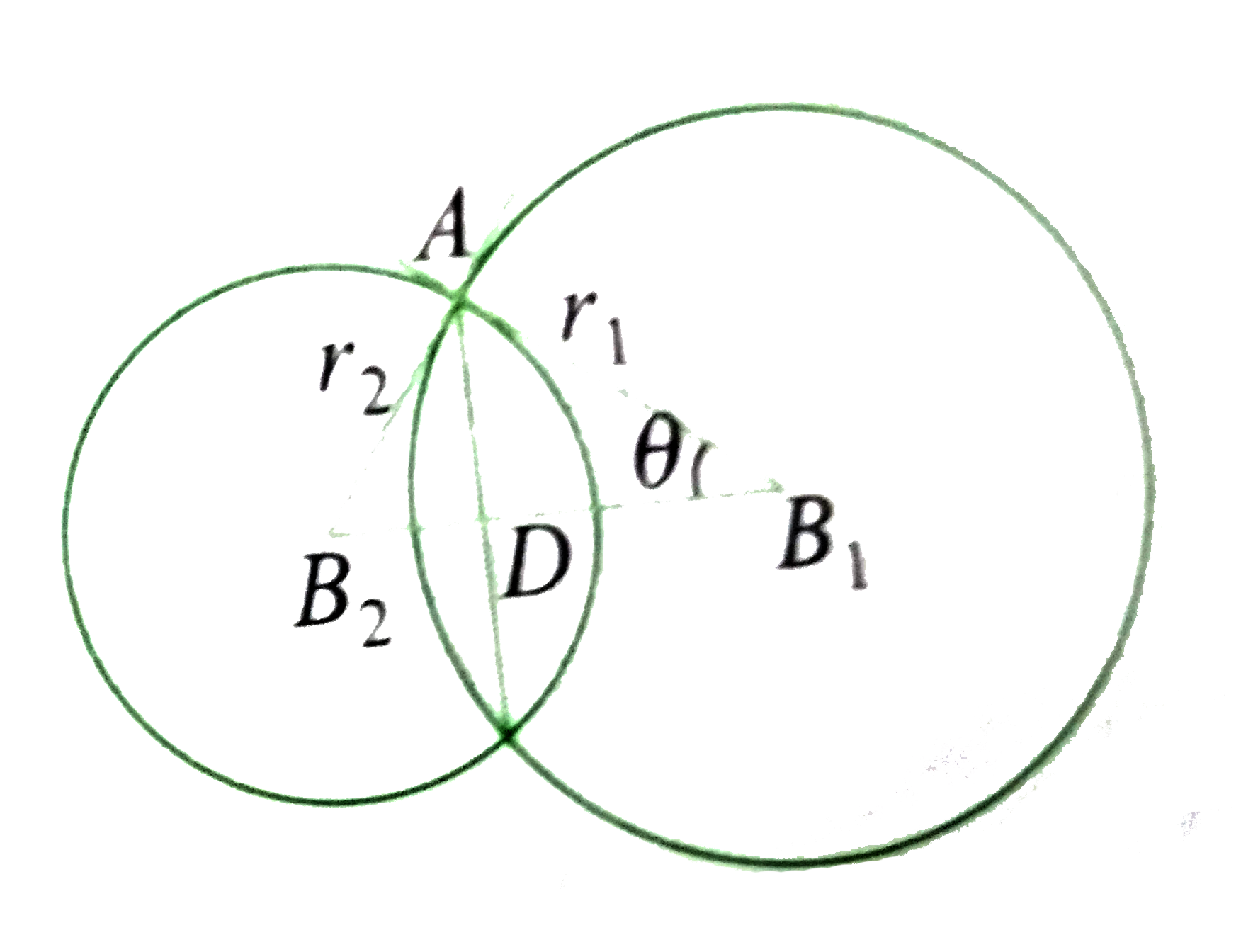
The circles having radii $r_{1} a n d r_{2}$ intersect orthogonally. The length of their common chord is $\frac{2 r_{1} r_{2}}{\sqrt{r 1^{2} + r 2^{2}}}$ (b) $\frac{\sqrt{r 1^{2} + r 2^{2}}}{2 r_{1} r_{2}}$ $\frac{r_{1} r_{2}}{\sqrt{r 1^{2} + r 1^{2}}}$ (d) $\frac{\sqrt{r 1^{2} + r 1^{2}}}{r_{1} r_{2}}$

A

$\frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$

B

$\frac{\sqrt{r_{2}^{2} + r_{1}^{2}}}{2 r_{1} r_{2}}$

C

$\frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$

D

$\frac{\sqrt{r_{2}^{2} + r_{1}^{2}}}{r_{1} r_{2}}$

Text Solution

Verified by Experts

The correct Answer is:1

Let $∠ A B_{1} B_{2} = θ$ Then,
$A D = r_{1} sin θ$ ( In $Δ A D B_{1})$
and $A D = r_{2} cos θ (ln Δ A D B_{2})$
$∴ A D^{2} (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}}) = 1$
or $A D = \frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
Thus, length of common chord $= \frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{1}^{2}}}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}} + \frac{1}{r_{3}^{2}} + \frac{1}{r^{2}} =$
A $\frac{a^{2} + b^{2} + c^{2}}{s^{2}}$
B $\frac{Σ a^{2}}{S^{2}}$
C $4 R$
D $4 R$

CENGAGE PUBLICATION-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile