Two circle with radii $r_{1}$ and $r_{2}$ respectively touch each other externally. Let $r_{3}$ be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is true

A

$\frac{1}{\sqrt{a}} - \frac{1}{\sqrt{b}} = \frac{1}{\sqrt{c}}$

B

$c = \frac{2 a b}{a + b}$

C

$\frac{1}{\sqrt{a}} + \frac{1}{\sqrt{b}} = \frac{1}{\sqrt{c}}$

D

$c = \frac{2 a b}{\sqrt{a} + \sqrt{b}}$

Text Solution

Verified by Experts

The correct Answer is:3

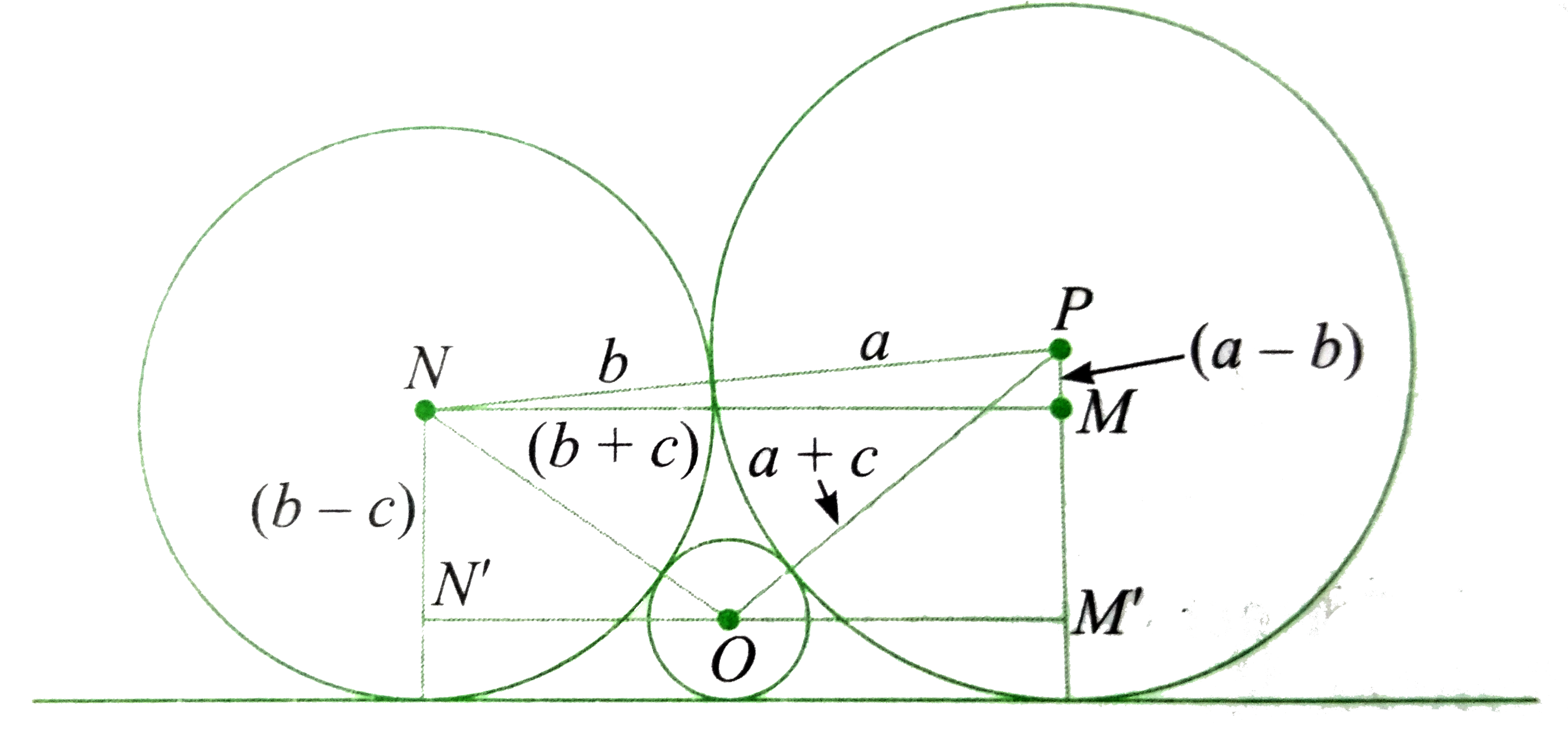
$∵ M' N' = M N$
Now, $M N = \sqrt{{(a + b)}^{2} + {(a - b)}^{2}} = \sqrt{4 a b}$
$N' O = \sqrt{{(b + c)}^{2} - {(b - c)}^{2}} = \sqrt{4 b c}$
$M' O = \sqrt{{(b + c)}^{2} - {(a - c)}^{2}} = \sqrt{4 a c}$
Now, $N' O + M' O = M N$
$\Rightarrow 2 \sqrt{a b} = 2 \sqrt{b c} + 2 \sqrt{a c}$
Dividing by $\frac{1}{\sqrt{a b c}}$ , we get
$\frac{1}{\sqrt{c}} = \frac{1}{\sqrt{a}} + \frac{1}{\sqrt{b}}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cm
B50 cm
C40 cm
D30 cm
Question 2 - Select One
Two circles of radii $r_{1}$ and $r_{2}, r_{1} > r_{2} \geq 2$ touch each other externally. If $θ$ be the angle between the direct common tangents, then,
A $θ = {sin}^{- 1} (\frac{r_{1} + r_{2}}{r_{1} - r_{2}})$
B $θ = 2 {sin}^{- 1} (\frac{r_{1} - r_{2}}{r_{1} + r_{2}})$
C $θ = {sin}^{- 1} (\frac{r_{1} - r_{2}}{r_{1} + r_{2}})$
Dnone of these
Question 3 - Select One
Two circles of radii 8 cm and 6 cm touch each other externally. The length of the direct common tangent is:
8 सेमी तथा 6 सेमी त्रिज्याओं वाले दो वृत्त एक-दूसरे को बाहर से स्पर्श करते हैं | प्रत्यक्ष उभयनिष्ठ स्पर्श रेखा की लंबाई कितनी है ?
A20
B24
C $13.86$
D $10.12$

CENGAGE PUBLICATION-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile