Question

A tangent to the ellipse $x^2+4y^2=4$ meets the ellipse $x^2+2y^2=6$ at P&Q.

Explanation

The given ellipse are
`(x^(2))/(4)+(y^(2))/(1)=1" "(1)`
and `(x^(2))/(6)+(y^(2))/(3)=1" "(2)`

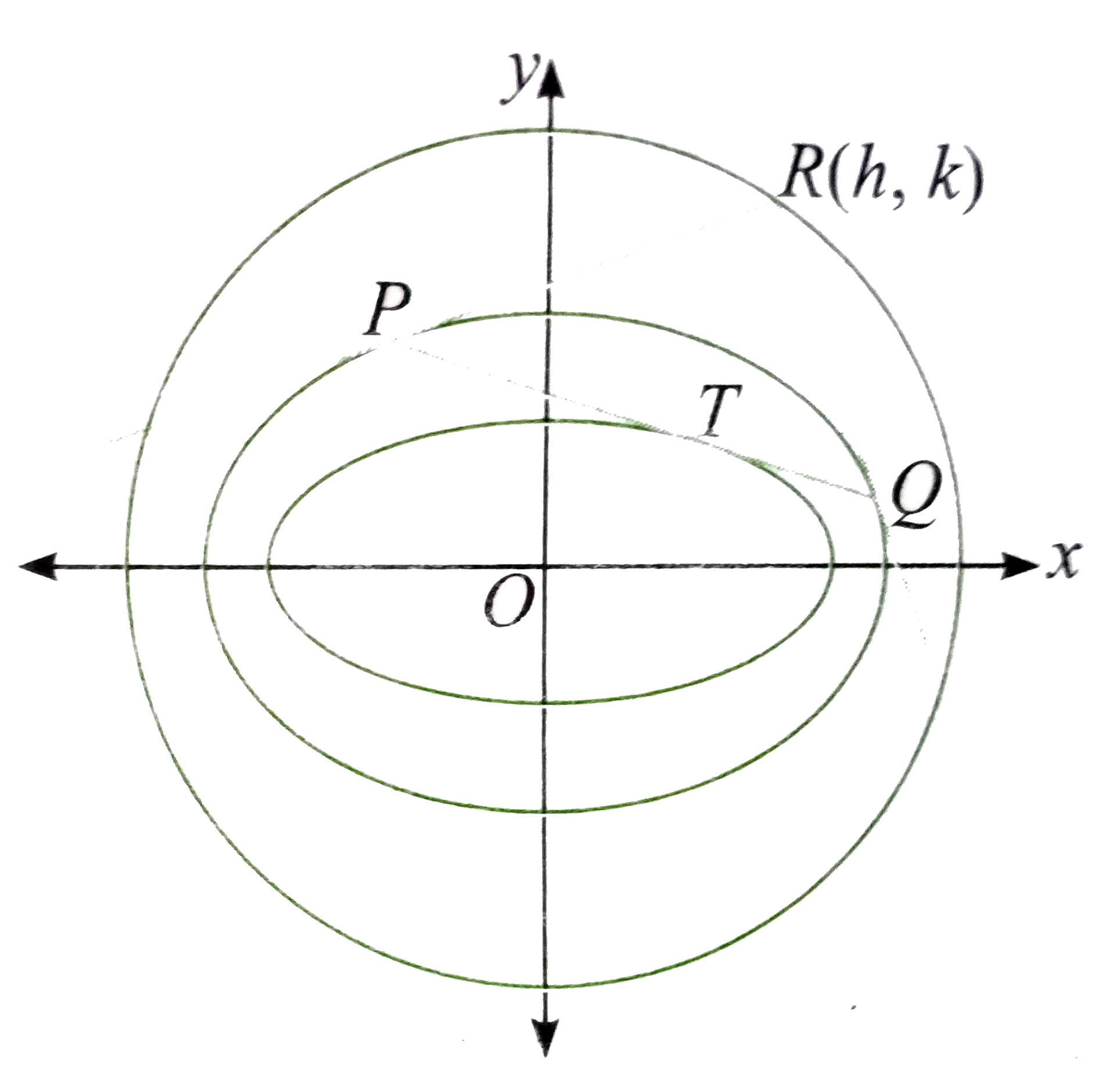
Then the equation of tangent to (1) at point `T(2 cos theta, sin theta)` is given by
`(xcostheta)/(2)+(y sin theta)/(1)=1" "(3)`
Let this tangent meet the ellipse (2)at P and Q . Let the tangents drawn to ellipse (2)at P and Q meet each other at R(h,k) .
Tehn PQ is the chord of contact of ellipse (2) with respect to teh point (R(h,k) and is given by
`(xh)/(6)+(yk)/(3)=1`
Clearly, (3) and (4) represent the same line and, hence should be identical.
Therefore, comapring the ratio of coefficients , we get
`((costheta)//2)/(h//6)=(sin theta)/(k//3)=(1)/(1)`
or ` h=3 cos theta, k=3 sin theta`
or `h^(2)+k^(2)=9`
Therfore, hte locus of (h,k) is `x^(2)+y^(2)=9`
Which is the director circle of he ellipse `(x^(2))/(6)+(y^(2))/(3)=1`
and we know that the director circle is the locus of the point of intersection of the tangents which are at right angle.
Thus, tangents at P and Q are perpendicular