The tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce is Solution in Bengali
12
16
20
8
Tangent at P(4cosθ,4sinθ)→x2+y2=16 is xcosθy+sinθ=4 (1)
The equation of AP is y=sinθcosθ−1(x−4) (2)
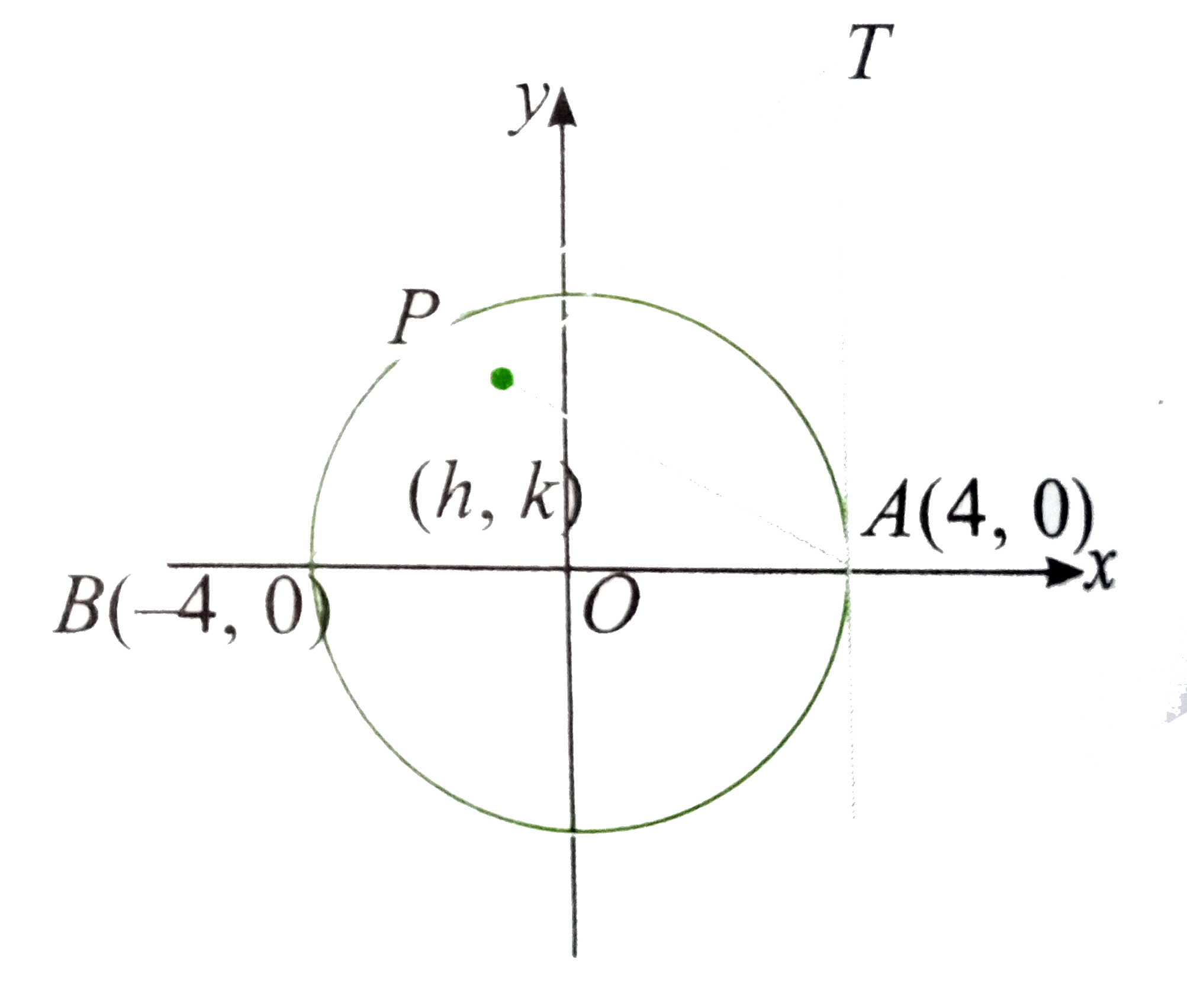
From (1), the coordinates of the point T are given by
(4,4(1−cosθ)sinθ)
The equation of BT is y=1−cosθ2sinθ(x+4) (3)
Let (h,k) be the point of intersection of the lines (2), and (3). Then we have
k2=−12(h2−16)
or h216+y28=1
Therefore, the locus of (h,k) is x216+y28=1
Which is an ellipse with eccehntrically e=1/√2
Sum of focal distance of any points is 2a=8
Considering the circle x2+y2=a2, we find the that the eccentricity of the ellipse is 1√2 which is contant and does not change by changing the radius of the circle
Similar Questions
A tangent to the ellipes x225+y216=1 at any points meet the line x=0 at a point Q Let R be the image of Q in the line y=x, then circle whose extremities of a dameter are QandR passes through a fixed point, the fixed point is
03:12View SolutionThe tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The locus of the intersection of AO and BT is a conic whosee eccentricity is04:15View SolutionThe tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
The sum of focal distance of any point on the curce is03:12View SolutionThe tagents at any point P of the circle x2+y2=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A.
Which of the following does not change by changing the radius of the circle ?04:29View Solutionवृत x2+y2=a2 के किसी बिन्दु P पर स्पर्श रेखा, स्थिर बिन्दु A (a. 0) पर बनी स्पर्श रेखा, T पर मिलती है तथा T को B से मिलाते है, जो A से गुजरने वाले व्यास का दूसरा सिरा है। सिद्ध कीजिए कि AP और BT के प्रतिच्छेद बिन्दुका बिन्दुपथ एक दीर्घवृत्त होगा, जिसकी उत्केन्द्रता 1√2 है।
07:04View SolutionIf the diameter through any point P of a parabola meets any chord in A and the tangent at the end of the chord meets the diameter in B and C, then prove that PA2=PB.PC
11:15View SolutionA tangent to the ellipes x^2/25+y^2/16=1 at any points meet the line x=0 at a point Q Let R be the image of Q in the line y=x, then circle whose extremities of a dameter are Q and R passes through a fixed point, the fixed point is
05:20View SolutionThe tangents at any point P of the circle x^(2)+y^(2)=16 meets the tangents at a fixed point A at T. Point is joined to B, the other end of the diameter, through, A. The sum of focal distance of any point on the curce is
05:56View Solution

