Match the statements/expressions in List I with statements/expressions in List II.

Text Solution
The correct Answer is:a→q,s
We have 2sin2θ+sin22θ=2
⇒2sin2θ+4sin2θcos2θ=2
⇒sin2θ+2sin2θ(1−sin2θ)=1
⇒3sin2θ−2sin4θ−1=0
⇒sinθ=±1√2,±1
⇒θ=π4,π2
Note : Solutions of the remaining parts are given in their respective chapters.
|
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Linked comprehension type)
1 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Knowledge Check
Match the statements/expressions given in List I with the values given in List II.
 AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
Match the conic in List I with the statements/expressions in List II.

View SolutionMatch the statements/expressions given in List ( with the value given in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionMatch the statements given in the List-I with the equations given in List-II.
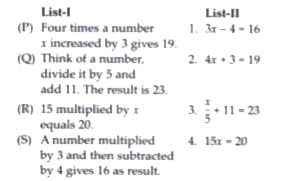
View SolutionMatch the statements given in List I with the values given in List II.

View SolutionMatch the statements in List I the appropriate answer in List II.

View Solution



