The direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as $l_{1}, m_{1}, n_{1}, l_{2}, m_{2}, n_{2}$ and $l_{3}, m_{3}, n_{3}$ are

A

$l_{1} + l_{2} + l_{3}, m_{1} + m_{2} + m_{3}, n_{1} + n_{2} + n_{3}$

B

$\frac{l_{1} + l_{2} + l_{3}}{\sqrt{3}}, \frac{m_{1} + m_{2} + m_{3}}{\sqrt{3}}, \frac{n_{1} + n_{2} + n_{3}}{\sqrt{3}}$

C

$\frac{l_{1} + l_{2} + l_{3}}{3}, \frac{m_{1} + m_{2} + m_{3}}{3}, \frac{n_{1} + n_{2} + n_{3}}{3}$

D

none of these

Text Solution

Verified by Experts

The correct Answer is:B

Since the three lines are mutually perpendicular
$∴ l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0$
$l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3} = 0$
$l_{3} l_{1} + m_{3} m_{1} + n_{3} n_{1} = 0$
Also $l_{1}^{2} + m_{1}^{2} = 1, l_{2}^{2} + m_{2}^{2} + n_{2}^{2} = 1 .$
$l_{3}^{2} + m_{3}^{2} + n_{3}^{2} = 1$
Now, ${(l_{1} + l_{2} + l_{3})}_{1}^{2} + {(m_{1} + m_{2} + m_{3})}_{1}^{2} + {(n_{1} + n_{2} + n_{3})}_{1}^{2}$
$= (l_{1}^{2} + m_{1}^{2} + n_{1}^{2} + (l_{2}^{2} + m_{2}^{2} + n_{2}^{2}) + (l_{3}^{2} + m_{3}^{2} + n_{3}^{2}) + 2 (l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2}) + 2 (l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3}) + 2 (l_{3} l_{1} + m_{3} m_{1} + n_{3} n_{1}) = 3$
$\Rightarrow {(l_{1} + l_{2} +_{3})}_{1}^{2} + {(m_{1} + m_{2} + m_{3})}_{1}^{2} + {(n_{1} + n_{2} + n_{3})}_{1}^{2} + {(m_{1} m_{2} + m_{3})}_{1}^{2} + {(n_{1} + n_{2} + n_{3})}_{1}^{2} = 3$
Hence, direction cosines of required line are
$\frac{l_{1} + l_{2} + l_{3}}{\sqrt{3}}, \frac{m_{1} + m_{2} + m_{3}}{\sqrt{3}}, \frac{n_{1} + n_{2} + n_{3}}{\sqrt{3}}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - All Questions
674videos
APPLICATION OF DERIVATIVES

Similar Questions

Knowledge Check

Question 1 - Select One
The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as $(l_{1}, m_{1}, n_{1}), (l_{2}, m_{2}, n_{2}), (l_{3}, m_{3}, n_{3})$ are
Athe direction cosines of three mutually perpendicular lines
Bthe direction ratios of three mutually perpendicular lines which are not direction cosines.
Cthe direction cosines of three lines which need not be perpendicular
Dthe direction of three lines which need not be perpendicular
Question 2 - Select One
Two lines with direction cosines $l_{1}, m_{1}, n_{1} and l_{2}, m_{2}, n_{2}$ are at right angle of
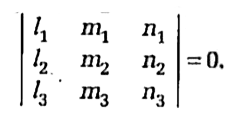
A $l_{1} l_{2} - m_{1} m_{2} - n_{1} n_{2} = 0$
B $l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0$
C $l_{2} = l_{2}, m_{1} = m_{2}, n_{1} = n_{2}$
D $\frac{l_{1}}{l_{2}} = \frac{m_{1}}{m_{2}} = \frac{n_{1}}{n_{2}}$
Question 3 - Select One
If $l_{1}, m_{1}, n_{1}, l_{2}, m_{2}, n_{2} and l_{3}, m_{3}, n_{3}$ are direction cosines of three mutuallyy perpendicular lines then, the value of $∣ ∣ ∣ ∣ \begin{matrix} l_{1} & m_{1} & n_{1} l_{2} & m_{2} & n_{2} l_{3} & m_{3} & n_{3} \end{matrix} ∣ ∣ ∣ ∣$ is
A $l_{3} m_{3} n_{3}$
B $\pm 1$
C $l_{1} m_{1} n_{1}$
D $l_{2} m_{2} n_{2}$

CENGAGE PUBLICATION-3D COORDINATION SYSTEM -DPP 3.1

Home
Ask Doubt
Profile