ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.Ar(△ABD)=k2,ar(△BCD)=k3 then ar(△ACD) is
A
√k21+k22+k23
B
√k1k2k3k1+k2+k3
C
√∣∣k21+k22−k23∣∣
D
√∣∣k22−k21−k23∣∣
Text Solution
The correct Answer is:C
Let us suppose that A is origin .
ar(△ABC)2+ar(△ACD)2+ar(△ABD)2=ar(△BCD)2
⇒ar(△ACD)=√∣∣k21+k22−k23∣∣
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
A√k21+k22+k23B√k1k2k3k21+k22+k23C√∣∣(k21+k22−k23)∣∣D√∣∣(k21−k22−k23)∣∣In △ABC, if Rr≤2, and a=2, then △ is equal to (△=ar(△ABC)).
A3B9C√3D√34If △ABC~△DEF,ar(△DEF)=100cm2andABDE=12, then ar(DABC) is
A50cm2B25cm2C4cm2D200cm2
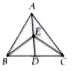
In the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View SolutionIf △ABC - △PQR and BCQR = 14 then ar(△PQR)ar(△ABC) =
View Solution