If $x^{2} + 2 a x + a < 0 \forall x \in [1, 2],$ the find the values of $a$ .

Text Solution

Verified by Experts

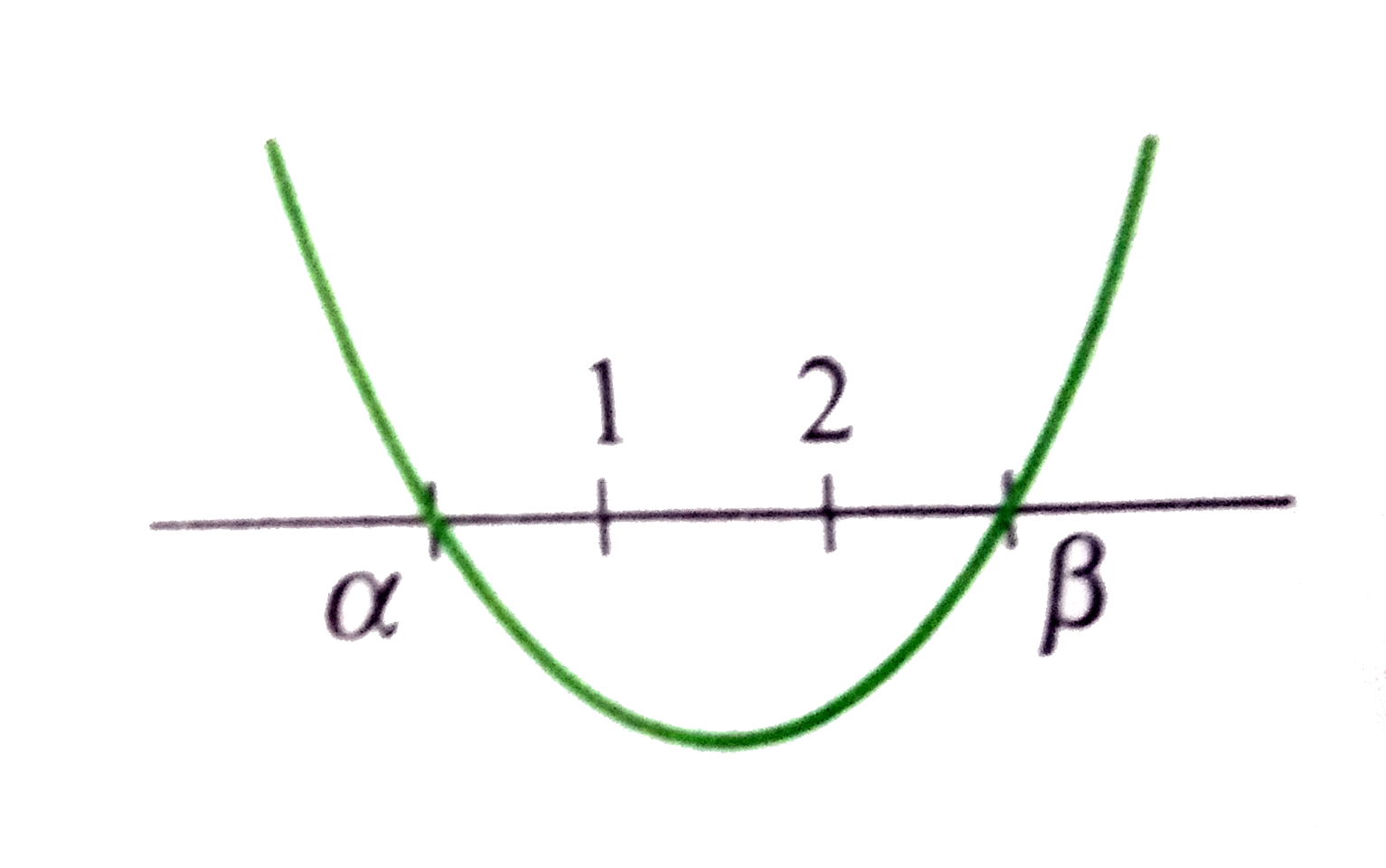
Given ,
$x^{2} + 2 a x + a < 0 . \forall x \in$ [1, 2]
Hence, 1 and 2 lie between the roots of the equation
$x^{2} + 2 a x + a = 0$
$\Rightarrow f (1) < 0 and f (2) < 0$
$\Rightarrow 1 + 2 a + a < 0, 4 + 4 a + a < 0$
$\Rightarrow a < - \frac{1}{3}, a < - \frac{4}{5}$
$\Rightarrow a \in (- \infty, - \frac{4}{5})$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $(x^{2} - 2 | x |) (| 2 x | - 2) - 9 (\frac{2 | x | - 2}{x^{2} - 2 | x |}) \leq 0$ then
A $x \in (- \infty, - 1] \cup (0, 1] \cup (2, 3]$
B $x \in (- \infty, - 1] \cup (2, 3] \cup {1}$
C $x \in (- \infty, 3]$
D $x \in [- 3, - 2) \cup [- 1, 0) \cup (0, 1] \cup (2, 3]$
Question 2 - Select One
If $∣ ∣ x^{2} - 2 x + 2 ∣ ∣ - ∣ ∣ 2 x^{2} - 5 x + 2 ∣ ∣ = ∣ ∣ x^{2} - 3 x ∣ ∣$ then the set of values of x is
A $(- \infty, 0] \cup [3, 00)$
B $[0, \frac{1}{2}] \cup [2, 3]$
C $(- \infty, 0] \cup [\frac{1}{2}, 2] \cup [3, \infty)$
D $[0, 2] \cup [3, \infty)$
Question 3 - Select One
The factors of ${(x^{2} + 2 x)}^{2} - 3 (x^{2} + 2 x) - y (x^{2} + 2 x) + 3 y$ are
A $(x - 1) (x + 3) (x^{2} + 2 x + y)$
B $(x - 1) (x + 3) (x^{2} + x - y)$
C $(x - 1) (x - 3) (x^{2} + 2 x - y)$
DNone of the above

CENGAGE PUBLICATION-THEORY OF EQUATIONS-ILLUSTRATION

Home
Ask Doubt
Profile