Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0Solution in Bengali
Let f(x)=x2+bax+ca .
Accounting to the questions, we have the following graph.
From the graph.
f(−1)<0andf(1)<0
⇒1+ca−ba<0and1+ca+ba<0
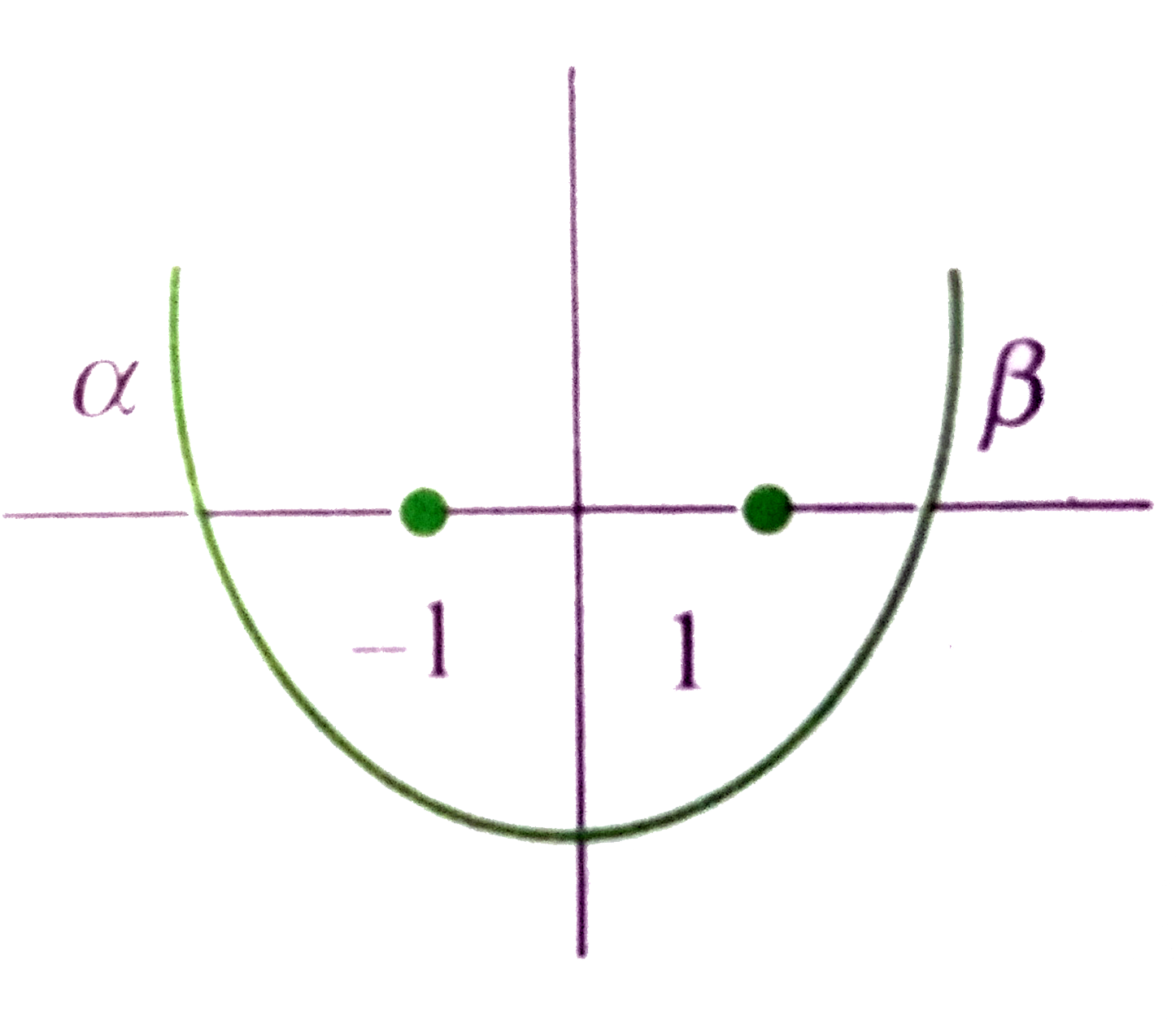
⇒1+ca+∣∣∣ba∣∣∣<0 .
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.139videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Single Correct Answer Type : Exercise89videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.118videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Find the values of a if x2−2(a−1)x+(2a+1)=0 has positive roots.
06:57View SolutionThe value of expression x4−8x3+18x2−8x+2 when x=2+√3
04:39View SolutionLet a is a real number satisfying a3+1a3=18 . Then the value of a4+1a4−39 is ____.
12:31View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
13:43View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
03:37View SolutionConsider two complex numbers αandβ as α=[(a+bi)/(a−bi)]2+[(a−bi)/(a+bi)]2, where a ,b , in R and β=(z−1)/(z+1),where|z|=1, then find the correct statement: both αandβ are purely real both αandβ are purely imaginary α is purely real andβ is purely imaginary β is purely real and α is purely imaginary
03:03View SolutionIf αandβ,αandγ,αandδ are the roots of the equations ax2+2bx+c=0,2bx2+cx+a=0adncx2+ax+2b=0, respectively, where a, b, and c are positive real numbers, then α+α2= a.abc b. a+2b+c c. −1 d. 0
02:32View SolutionConsider two complex numbers alphaa n dbeta as alpha=[(a+b i)//(a-b i)]^2+[(a-b i)//(a+b i)]^2 , where a ,b , in R and beta=(z-1)//(z+1), w here |z|=1, then find the correct statement: both alphaa n dbeta are purely real both alphaa n dbeta are purely imaginary alpha is purely real and beta is purely imaginary beta is purely real and alpha is purely imaginary
02:24View SolutionIf αandβ are the roots of ax2+bx+c=0andSn=αn+βn, then aSn+1+bSn+cSn−1=0 and hence find S5.
01:49View SolutionIf αandβ,αandγ,αandδ are the roots of the equations ax2+2bx+c=0,2bx2+cx+a=0adncx2+ax+2b=0, respectively, where a, b, and c are positive real numbers, then α+α2= a.abc b. a+2b+c c. −1 d. 0
02:57View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0
03:58View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα<−1andβ>1 , then show that 1+ca+∣∣∣ba∣∣∣<0
06:56View SolutionIf α is a real root of the quadratic equation ax2+bx+c=0andβ ils a real root of −ax2+bx+c=0, then show that there is a root γ of equation (a/2)x2+bx+c=0 whilch lies between aandβ.
03:55View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩−1 , then show that 1+ca+∣∣∣ba∣∣∣<0
03:08View SolutionIf αandβ are roots of the quadratic equation ax2+bx+c=0 and a+b+c>0,a−b+c>0&c<0,then[α]+[β] is equal to (where [.] denotes the greatest integer function) (a)10 (b) −3 (c) −1 (d) 0
04:37View SolutionIf α is a real root of the quadratic equation ax2+bx+c=0andβ ils a real root of −ax2+bx+c=0, then show that there is a root γ of equation (a/2)x2+bx+c=0 whilch lies between α&β
02:19View Solution

