Let Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.Solution in Bengali
The correct Answer is:65
Sk=k1−1k+1=k+1
aum10k=1Sk=10∑k=1(k+1)=10×112+10=65
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES ( JEE MAIN )(SINGLE CORRECT ANSWER TYPE )
16 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES ( JEE ADVANCED )(SINGLE CORRECT ANSWER TYPE )
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - EXERCIESE ( MATRIX MATCH TYPE )
3 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
Similar Questions
The sum to infinity of the series 1+23+632+1033+1434...... is (1) 2 (2) 3 (3) 4 (4) 6
View SolutionLet a1,a2,a3,... be a harmonic progression with a1=5anda20=25. The least positive integer n for which an<0, is
View SolutionIf αandβ are roots of the equation x2−8x+4=0, then match the following lists :

View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionLet ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionFor each positive integer k, let Sk denote the increasing arithmetic sequence of integers whose firstterm is 1 and whose common difference is k. For example, S3 is the sequence 1,4,7,10.......Find thenumber of values of k for which Sk contain the term 361.
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
View SolutionLet Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
View SolutionLet SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
View Solutionयदि एक अनंत गुणोत्तर श्रेणी जिसका प्रथम पद k और सरवणुपात kk+1(k>0) का योग प्रदर्शित करता है तब ∞∑k=1(−1)kSkका मान होगा
View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View SolutionLet Sk be the sum of first k terms of an A.P. What must this progression be for the ratio SkxSx to be independent of x?
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
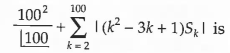 is
is
View Solution
