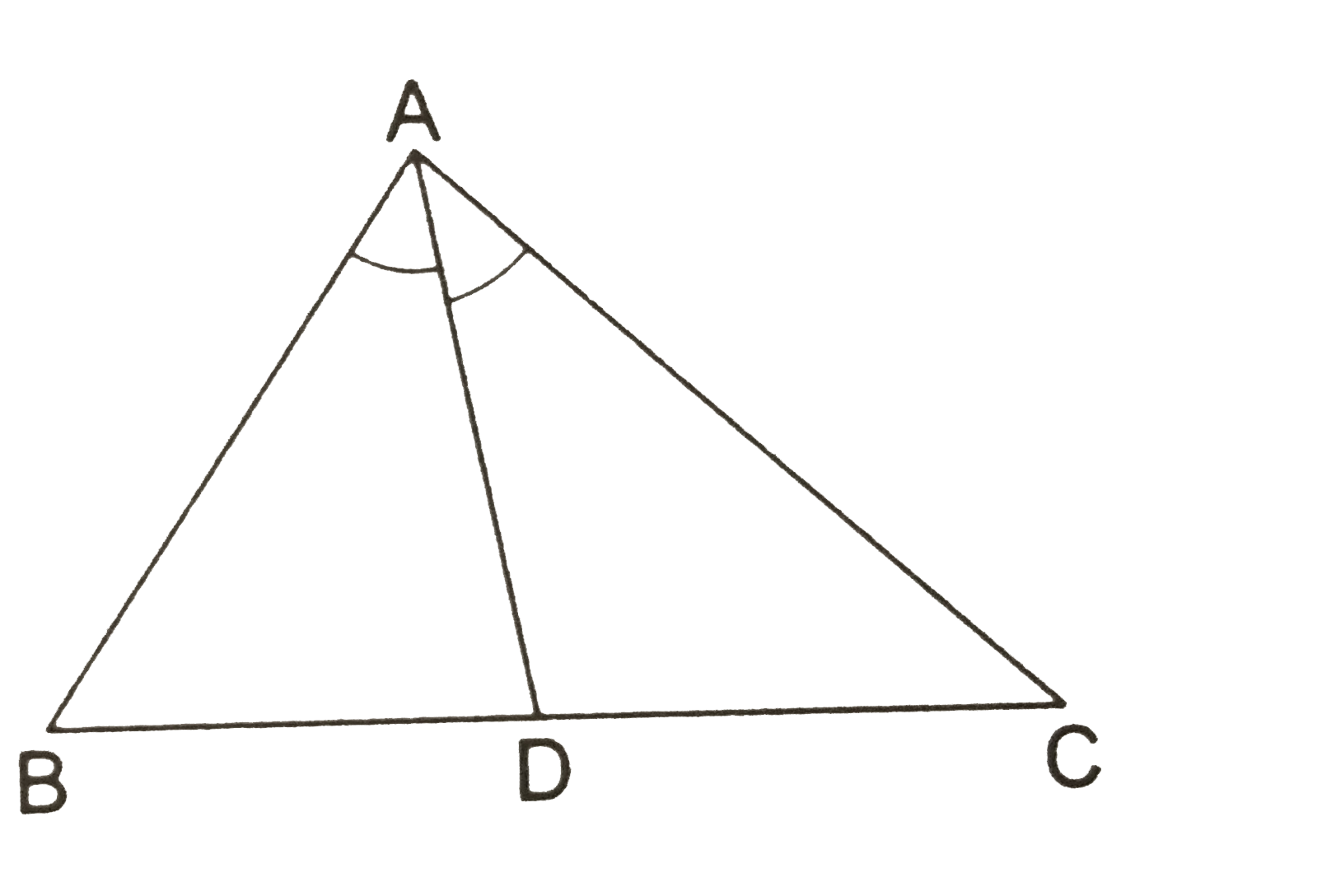
AD is the bisector of ∠A such that AD⊥BC. Then, find out whether △ABC is an isosceles triangle or not? Give appropriate reason.
Video Solution
|
Answer
Step by step video & image solution for AD is the bisector of angleA such that AD bot BC. Then, find out whether triangleABC is an isosceles triangle or not? Give appropriate reason. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PREP TEST 1 BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST 1 EXERCISE - SECTION-B
29 Videos
- PERIMETER AND AREA BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- PREP TEST 2 BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST 2 EXERCISE - SECTION-B
30 Videos
Similar Questions
Knowledge Check
In the figure, if ∠BAC=90∘ and AD⊥BC, then:
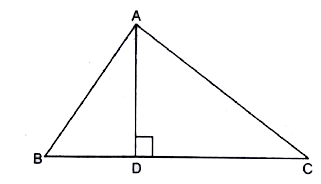 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2ΔABC is an equilateral triangle such that AD⊥ BC, then AD2=
A32DC2B2DC2C3CD2D4DC2The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. then
AAB:AC=BD:DCBAD:AC=AE:ABCAB:AD=AC:AEDAB:AB=AE:AC
If D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

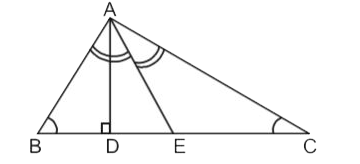
View SolutionIn the figure AE is the bisector of ∠A,AD⊥BC . Show that 2(∠ADE−∠EAC)=∠B+∠C
View SolutionIn a △ABC,AB = AC and AD⊥BC, then :
View SolutionIn △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
View SolutionLet ABC be a triangle with ∠B=90∘. Let AD be the bisector of ∠A with D on BC. Supose AC = 6 cm and the area of the triangle ADC is 10 cm2 . Then the length of BD in cm is equal to
View Solution