The angular speed of the Earth decreases with time. This pace is indicated by the observations of the occurrences of solar eclipse during this period. Let us assume that the length of the day uniformly increases by 0.001 s per century. Calculate the cumulative effect on the measure of time for a period of 10 centuries. (Express it in seconds).
To solve the problem, we need to calculate the cumulative increase in the length of the day over a period of 10 centuries, given that the length of the day increases by 0.001 seconds per century.
1. Identify the increase in length of the day per century:
- The problem states that the length of the day increases by 0.001 seconds per century.
2. Determine the total increase over 10 centuries:
- Since the increase is uniform, we can multiply the increase per century by the number of centuries.
- Total increase = Increase per century × Number of centuries
- Total increase = 0.001 seconds/century × 10 centuries
3. Perform the multiplication:
- Total increase = 0.001 seconds × 10 = 0.01 seconds
4. Express the cumulative effect:
- The cumulative effect on the measure of time over a period of 10 centuries is 0.01 seconds.
Final Answer:
The cumulative effect on the measure of time for a period of 10 centuries is 0.01 seconds.
---
- The problem states that the length of the day increases by 0.001 seconds per century.
- Since the increase is uniform, we can multiply the increase per century by the number of centuries.
- Total increase = Increase per century × Number of centuries
- Total increase = 0.001 seconds/century × 10 centuries
- Total increase = 0.001 seconds × 10 = 0.01 seconds
- The cumulative effect on the measure of time over a period of 10 centuries is 0.01 seconds.
The cumulative effect on the measure of time for a period of 10 centuries is 0.01 seconds.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - GENERAL EXERCISE
14 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
8 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - MANDATORY EXERCISE (EXERCISE SET II) MULTIPLE-CHOICE QUESTIONS WITH ONE OR MORE THAN ONE CORRECT ANSWERS
4 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
9 Videos
Similar Questions
If the length of a seconds pendulum is first decreased by 10 cm and its time period is determined and then increased by 20 cm and the time period is once again determined, find the ratio of the time periods in two cases. (Take g=9.8ms−2)
View SolutionIf the length of a seconds pendulum is first decreased by 10 cm and its time period is determined and then increased by 20 cm and the time period is once again determined, find the ratio of the time periods in two cases. (Take g=9.8ms−2)
View Solution
Knowledge Check
Assuming the length of the day uniformly increases by 0.001 second per century. Calculate the net effect on the measure of time over 20 centuries.
A3.2 hourB2.1 hourC2.4 hourD5 hourA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
The time periods - hence the frequencies (f) and the amplitudes (A) of the driven pendulums in steady state are measured. The variation of A wil f is correctly shown by the graph.A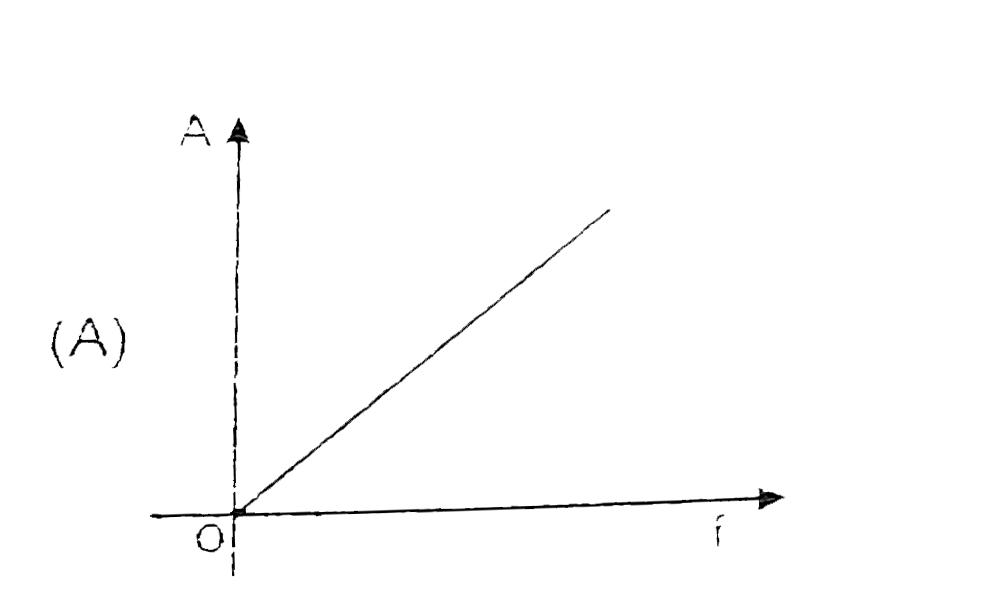 B
B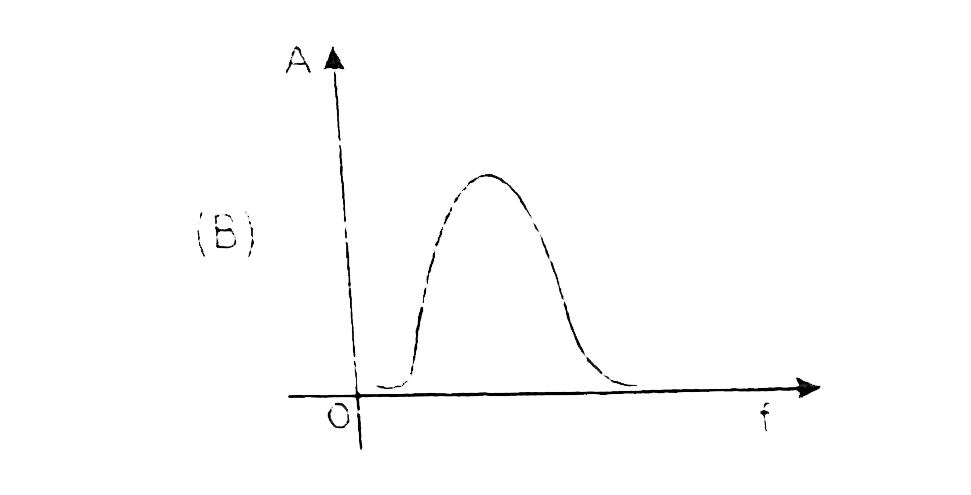 C
C D
D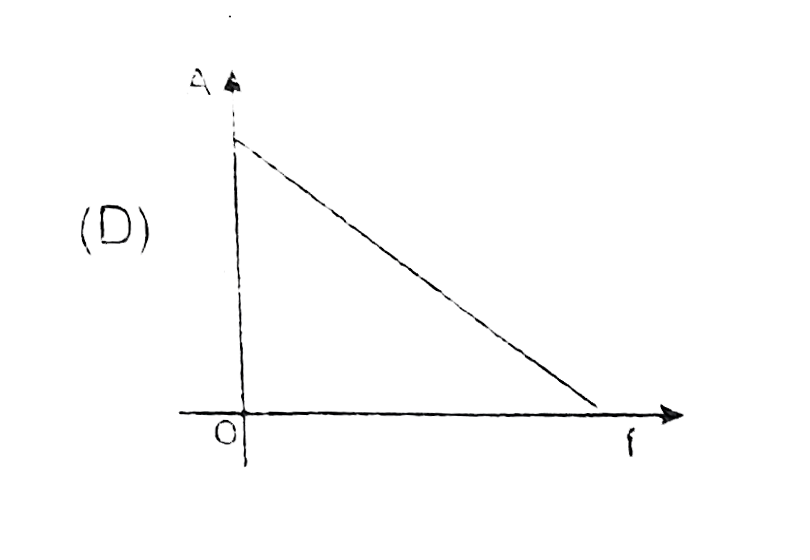
100 millicuries of radon which emits 5.5MeVα- particles are contained in a glass capillary tube 5cm long with internal and external diameters 2 and 6mm respectively Neglecting and effects and assuming that the inside of the uniformly irrandicated by the particles which are stopped at the surface calculate the temperature difference between the walls of aa tube when steady thermal conditions have been reached. Thermal conductivity of glass =0.025Calcm−2s−1C−1
Curie =3.7×1010 disintergration per second
J=4.18 joule Cal−1s
View SolutionWhen the sun appears to be just on horizon, it is in fact below the horizon. This is because the light from the sun bends when it enters the earth’s atmosphere. Let us assume that atmosphere is uniform and has index of refraction equal to μ. It extends upto a height h(<<R= radius of earth) above the earth’s surface. In absence of atmosphere how late would we see the sunrise compared to what we see now? Take time period of rotation of earth to be T. Calculate this time for following data
R=6400km,μ=1.0003,h=20km,T=24hr.
View SolutionTwo boys are holding a wire, standing 4 m apart. The wire sags in the shape of a circular arc with a sag of 1.0 m. The students rotate the wire about the horizontal line connecting their hands, as if they were playing jump rope. The boys rotate the wire at a speed of 4 revolutions per second. The earth’s magnetic field at the location is4×10–5 T. Calculate the rms value of emf developed between the ends of the wire. Assume that the shape of the wire is maintained as it is rotated.
View SolutionA metallic coil of N turns of radius resistance R, and inductance L is held fixed with its axis along a spatial uniform magnetic field ¯¯¯B whose magnitude is given by B0sin(ωt).
Write the equation for the current i in the coil.
(b) Assuming that in the steady state oscillates with the same frequency as the magnetic field, obtain the expression for i.
(c )Obtain the force per unit length. Further obtain its oscillatory part and the time-averaged compressional part.
(d) Calculate the time-averaged compressional force per unit length given that B0=1.00tesla,N=10a=10cm,ω=1000.0rads−1,R=10.0Ω,L−100,0mH.
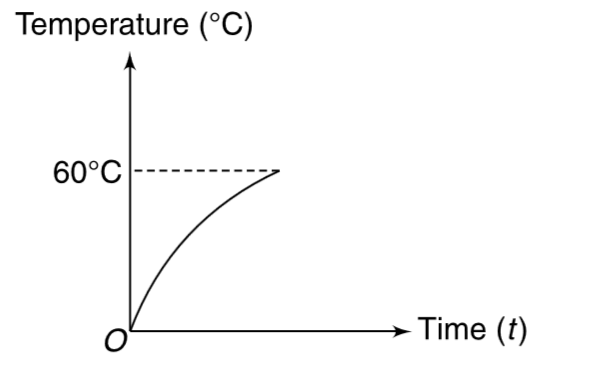
View SolutionA block is kept in a room which is at 20∘C. To raise the temperature of the block, heat is given to it at a constant rate of 600 watt (using an electric heater). The temperature of the block rises with time as shown in the graph. The slope of the graph at time t=0 is 3∘Cs−1. Once the temperature rises to 60∘C, the heater is switched off and another heater is switched on to maintain the temperature of the block at 60∘C. This new heater supplies heat at a constant rate of 100 watt. Assume that heat capacity of the block remains constant for the range of temperature involved.
(a) Explain why the slope of the given graph is decreasing with time.
(b) Calculate the heat capacity of the block.
(c) If the 100 W heater is also switched off, what will be initial rate of cooling of the block?
(d) Assuming that rate of heat loss by the block to the surrounding is proportional to difference in its temperature with surrounding, calculate the heat radiated per second by the block when it was at 30∘C.
View SolutionA long solenoid of length l=2.0 m , radius r=0.1 m and total number of turns N=1000 is carrying a current i0=20.0A. The axis of the solenoid conicides with the z-axis.
(a) State the expression for the magnetic field of the solenoid and calculate its value ? Magnetic field.
(b) Obtain the expression for the self - inductance (L) of the solenoid. Calcuate its value. Value of L .
( c) Calculate the energy stored (D) when the solenoid carries this current ?
(d) Let the resistance of the solenoid be R. It is connected to a battery of emf e. Obtain the expression for the current (i) in the solenoid.
(e) Let the solenoid with resistance R describe in part (d) be strecthed at a constant speed u ( l is increased but B and γ are constant ). State kirchhoff's second law for this cases. (Note: Do not solve for the current )
(f) Consider a time varying current i=i0cos(ωt) (where i0=20.0A) flowing in the solenoid. Obtain an expression for the electric field due to the current in the solenoid. (Note: Part(e) is not operative, i.e., the solenoid is not being stretched. )
(g) Consider t=π/2ωandω=200/πrad−s−1 in the previous part. Plot the magnitude of the electric field as a function of the radial distance from the solenoid. Also, sketch the electric lines of force.
View Solution
